
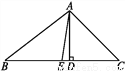
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sin B=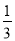 ,AD=1.
,AD=1.
求:(1)BC的长;
(2)tan∠DAE的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:湖北省大冶市金湖街办2017-2018学年八年级上学期第二次月考(12月)数学试卷 题型:解答题
分解因式:
(1)3x2y-6xy+3y (2)(a2+1)2-4a2.
(1)3y(x-1)2 ;(2)(a+1)2(a-1)2. 【解析】试题分析:(1)提公因式后用完全平方公式分解即可; (2)先用平方差公式,再用完全平方公式分解即可. 试题解析:【解析】 (1)原式==; (2)原式==.查看答案和解析>>
科目:初中数学 来源:辽宁省2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
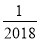 的相反数为( )
的相反数为( )
A. 2018 B. -2018 C. 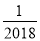 D.
D. 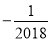
查看答案和解析>>
科目:初中数学 来源:浙江省湖州市吴兴区2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则劣弧AC的长( )
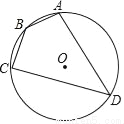
A. 8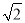 B. 4
B. 4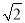 C. 2π D. π
C. 2π D. π
查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:解答题
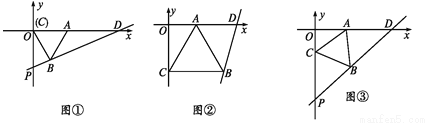
△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).
(1)如图①,当点C与点O重合时,求直线BD的表达式;
(2)如图②,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的☉B与y轴相切(切点为C)时,求点B的坐标;
(3)如图③,点C从点O沿y轴向下移动,当点C的坐标为C(0,-2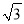 )时,求∠ODB的正切值.
)时,求∠ODB的正切值.
查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:填空题
△ABC中,AB=10 cm,AC=8 cm,BC=6 cm,以点B为圆心,6 cm为半径作☉B,则边AC所在的直线与☉B的位置关系是___.
相切 【解析】试题解析:∵△ABC中,AB=10cm,AC=8cm,BC=6cm, 则圆心到直线的距离即为BC的长6cm,等于圆的半径,则直线和圆相切. 故答案为:相切.查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:单选题
已知二次函数y=ax2+bx+c+2的图象如图,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )
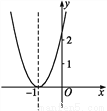
A. 1 B. 2 C. 3 D. 4
B 【解析】【解析】 ∵抛物线开口向上, ∴a>0, ∵对称轴在y轴左边, ∴b>0, ∵抛物线与y轴的交点在x轴的上方, ∴c+2>2, ∴c>0, ∴abc>0, ∴结论①不正确; ∵二次函数y=ax2+bx+c+2的图象与x轴只有一个交点, ∴△=0, 即b2﹣4a(c+2)=0, ∴b2﹣4ac=8a>0, ...查看答案和解析>>
科目:初中数学 来源:宁夏2017-2018学年度上期七年级数学期末综合检测模拟试卷 题型:填空题
当k=____时,代数式x2 - 3kxy - 3y2+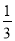 xy - 8中不含xy项.
xy - 8中不含xy项.
查看答案和解析>>
科目:初中数学 来源:2017年四川省数学七年级(上)期末数学试卷 题型:解答题
如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1) 写出∠DOE的补角;
(2)若∠BOE = 62°,求∠AOD和∠EOF的度数;
(3)射线OD与OF之间的夹角是多少?
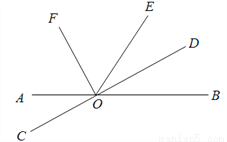
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com