练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    方程x2=x的解是__．

    x1=0，x2=1 【解析】x2-x=0. x(x-1)=0, x=0,x-1=0, x1=0，x2=1.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型：单选题

    已知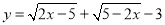，则2xy的值为

    A. -15 B. 15 C. -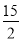 D.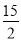

    【答案】A

    【解析】试题分析：根据题意可得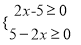： ，解得x=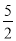，所以y=-3，所以2xy=2×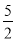×（-3）=-15，故选：A．

    考点：二次根式有意义的条件．

    【题型】单选题
    【结束】
    5

    在平面直角坐标系中，点P（﹣2，3）关于x轴的对称点在（　　）

    A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

    C 【解析】试题分析：首先根据关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数可得对称点的坐标，再根据坐标符号判断所在象限即可． 【解析】 点P（﹣2，3）关于x轴的对称点为（﹣2，﹣3）， （﹣2，﹣3）在第三象限． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：解答题

    解方程：4x(2x+1)=3(2x+1).(因式分解法)

    x1=﹣或x2=. 【解析】4x(2x+1)﹣3(2x+1)=0，(2x+1)(4x﹣3)=0， ∴2x+1=0或4x﹣3=0， 解得：x1=﹣或x2=.

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：填空题

    方程x2﹣9=0的解是______．

    x=±3． 【解析】x2﹣9=0 (x-3)(x+3)=0 所以x1=3，x2=-3.

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：填空题

    方程x(x-1)=x的解是_________．

    x1=0，x2=2 【解析】x(x-1)-x=0， x (x-1-1)=0, x (x-2)=0, 所以x1=0，x2=2.

    查看答案和解析>>

    科目：初中数学 来源：江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型：解答题

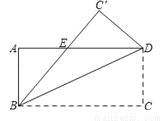
    如图，将长方形ABCD沿对角线BD折叠，使点C落在C′处，BC′交AD于点E．

    （1）试判断△BDE的形状，并说明理由；

    （2）若AB=4，AD=8，求△BDE的面积．

    （1）△BDE是等腰三角形；（2）10． 【解析】试题分析：（1）由折叠可知，∠CBD=∠EBD，再由AD∥BC，得到∠CBD=∠EDB，即可得到∠EBD=∠EDB，于是得到BE=DE，等腰三角形即可证明； （2）设DE=x，则BE=x，AE=8﹣x，在Rt△ABE中，由勾股定理求出x的值，再由三角形的面积公式求出面积的值． 【解析】 （1）△BDE是等腰三角形． 由折叠...

    查看答案和解析>>

    科目：初中数学 来源：江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型：填空题

    若函数y=（m+3）x2m+1+4x﹣2（x≠0）是关于x的一次函数，m_______．

    -3，0， ． 【解析】根据一次函数的定义可得：2m+1=1，m+3+4≠0或m+3=0或2m+1=0， 解得：m=0或m=-3或m=-， 故答案为：0，-3或-.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省中考数学模拟试卷 题型：解答题

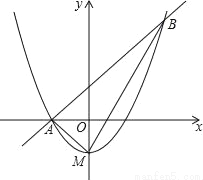
    如图，顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点，且点A在x轴上，点B的横坐标为2，连结AM、BM．

    （1）求抛物线的函数关系式；

    （2）判断△ABM的形状，并说明理由；

    （3）把抛物线与直线y=x的交点称为抛物线的不动点．若将（1）中抛物线平移，使其顶点为（m，2m），当m满足什么条件时，平移后的抛物线总有不动点．

    （1）抛物线解析式为y=x2﹣1；（2）△ABM为直角三角形．理由见解析；（3）当m≤时，平移后的抛物线总有不动点． 【解析】试题分析：（1）分别写出A、B的坐标，利用待定系数法求出抛物线的解析式即可； 根据OA＝OM＝1，AC＝BC＝3，分别得到∠MAC＝45°，∠BAC＝45°，得到∠BAM＝90°，进而得到△ABM是直角三角形； （3）根据抛物线的平以后的顶点设其解析式为，...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年上学期苏州市初三数学期末综合检测 题型：填空题

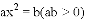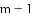
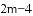
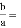    若一元二次方程的两个根分别是与，则________.

    4 【解析】由题意得 (m+1)+(2m-4)=0, 解之得 m=1. ∴m+1=2;2m-4=-2. ∵, ∴x1= ,x2=, ∴=2, =-2, ∴

    查看答案和解析>>

    同步练习册答案