练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    方程x2﹣9=0的解是______．

    x=±3． 【解析】x2﹣9=0 (x-3)(x+3)=0 所以x1=3，x2=-3.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型：解答题

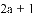
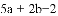
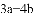
    已知的平方根是±3，的算术平方根是 4, 求的平方根．

    【答案】

    【解析】试题分析：根据已知得出2a+1=9，5a+2b-2=16，求出a b，代入求出即可．

    试题解析

    根据题意得：2a+1=32=9，5a+2b-2=16，
    即a=4，b=-1，
    ∴3a-4b=16，
    ∴3a-4b的平方根是±.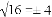

    【题型】解答题
    【结束】
    17

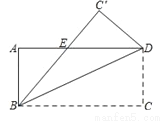
    如图，将长方形ABCD沿对角线BD折叠，使点C落在C′处，BC′交AD于点E．

    （1）试判断△BDE的形状，并说明理由；

    （2）若AB=4，AD=8，求△BDE的面积．

    （1）△BDE是等腰三角形；（2）10． 【解析】试题分析：（1）由折叠可知，∠CBD=∠EBD，再由AD∥BC，得到∠CBD=∠EDB，即可得到∠EBD=∠EDB，于是得到BE=DE，等腰三角形即可证明； （2）设DE=x，则BE=x，AE=8﹣x，在Rt△ABE中，由勾股定理求出x的值，再由三角形的面积公式求出面积的值． 【解析】 （1）△BDE是等腰三角形． 由折叠...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型：单选题

    若关于x的方程4x2﹣（2k2+k﹣6）x+4k﹣1=0的两根互为相反数，则k的值为（　　）

    A. B. ﹣2 C. ﹣2或 D. 2或

    B 【解析】根据题意得2k2+k?6=0， 解得k=?2或， 当k=时,原方程变形为4x2+5=0，△=0?4×4×5<0，此方程没有实数解， 所以k的值为?2. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：解答题

    解方程：2x2+5x﹣3=0．(因式分解法)

    x1=，x2=﹣3． 【解析】x2+5x﹣3=0, (2x﹣1)(x+3)=0， 2x﹣1=0或x+3=0， 所以x1=，x2=﹣3．

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：填空题

    方程(x+2)(x﹣3)=x+2的解是______．

    x1=﹣2，x2=4． 【解析】(x+2)(x﹣3)-(x+2)=0, (x+2)(x-3-1)=0, (x+2)(x-4)=0, 所以x1=-2，x2=4.

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：填空题

    已知(a+b)2-2(a+b)-3=0，则a+b=_______________.

    3或－1 【解析】把a+b看做一个整体,十字相乘, (a+b)2-2(a+b)-3=0, (a+b-3)(a+b+1)=0, a+b-3=0,a+b+1=0, 所以a+b=3,a+b=-1.

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：填空题

    方程x2=x的解是__．

    x1=0，x2=1 【解析】x2-x=0. x(x-1)=0, x=0,x-1=0, x1=0，x2=1.

    查看答案和解析>>

    科目：初中数学 来源：江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型：填空题

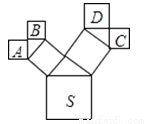
    如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A，B，C，D的面积和是49cm2，则其中最大的正方形S的边长为__________cm．

    7cm． 【解析】试题分析：根据正方形的面积公式，结合勾股定理，能够得出最大正方形的面积=正方形A，B，C，D的面积和=49cm2，所以最大的正方形S的边长为7cm.．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年上学期苏州市初三数学期末综合检测 题型：解答题

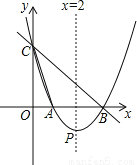
    如图，直线y=﹣x+3与x轴，y轴分别相交于点B，C，经过B，C两点的抛物线y=ax2+bx+c与x轴的另一交点为A，顶点为P，且对称轴是直线x=2．

    （1）求该抛物线的函数表达式；

    （2）请问在抛物线上是否存在点Q，使得以点B，C，Q为顶点的三角形为直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由；

    （3）过S（0，4）的动直线l交抛物线于M，N两点，试问抛物线上是否存在定点T，使得不过定点T的任意直线l都有∠MTN=90°？若存在，请求出点T的坐标；若不存在，请说明理由．

    （1）y=x2﹣4x+3；（2）存在；（3）存在点T（4，3）使得不过定点T的任意直线l都有∠MTN=90°． 【解析】试题分析：(1)根据坐标轴上点的坐标特征可求,,再根据待定系数法可求抛物线的函数表达式; (2)存在,分三种情况:过B点垂直BC的直线的解析式为y=x+b,过C点垂直BC的直线解析式为y=x+3,以BC为斜边,进行讨论可求点Q的坐标; (3)设M(x1,y1),...

    查看答案和解析>>

    同步练习册答案