练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若一次函数的自变量x的取值范围是﹣1＜x＜3时，函数值y的范围是﹣2＜y＜6，则此一次函数的解析式为（　　）

    A. y=2x B. y=﹣2x+4

    C. y=2x或y=﹣2x+4 D. y=﹣2x或y=2x﹣4

    C 【解析】设一次函数解析式为y=kx+b， （1）当x=﹣1时，y=﹣2；x=3时，y=6； 代入解析式得： ， 解得， ， ∴函数解析式为y=2x； （2）当x=﹣1时，y=6；x=3时，y=﹣2； 代入解析式得， ， 解得， ∴函数解析式为y=﹣2x+4． 故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省2017-2018学年七年级上学期第二次月考数学试卷 题型：填空题

    单项式﹣3πxyz2的系数是_____．

    ﹣3π． 【解析】根据单项式的概念，可知其系数为乘积中的系数，可得这个单项式的系数为-3π. 故答案为：-3π.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：填空题

    若关于x的一元二次方程（m+3）x2+5x+m2+2m－3=0有一个根是0，则m= ，另一根为 。

    m=1 【解析】∵方程（m+3）x2+5x+m2+2m-3=0有一个根为0，∴将x=0代入方程得：m2+2m-3=0， 即（m-1）（m+3）=0，解得：m1=1，m2=-3，又原方程为关于x的一元二次方程，m+3≠0，即m≠-3，则m=1．那么方程为4x2+5x=0，解得x=0或∴另一个根是．

    查看答案和解析>>

    科目：初中数学 来源：河南省郑州市郑东新区实验学校2017-2018学年八年级（上）期中数学试卷 题型：解答题

    如图，直线l1的解析表达式为：y=-3x+3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．

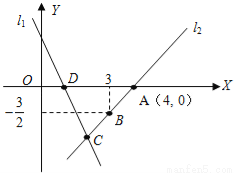
    （1）求点D的坐标；

    （2）求直线l2的解析表达式；

    （3）求△ADC的面积；

    （4）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．

    （1）D（1，0）；（2）；（3）；（4）P（6，3）． 【解析】试题分析：（1）已知l1的解析式，令y=0求出x的值即可； （2）设l2的解析式为y=kx+b，由图联立方程组求出k，b的值； （3）联立方程组，求出交点C的坐标，继而可求出S△ADC； （4）△ADP与△ADC底边都是AD，面积相等所以高相等，△ADC高就是点C到AD的距离． 【解析】 （1）由y=...

    查看答案和解析>>

    科目：初中数学 来源：河南省郑州市郑东新区实验学校2017-2018学年八年级（上）期中数学试卷 题型：填空题

    一次函数y=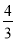x+4分别交x轴、y轴于A、B两点，在x轴上取一点，使△ABC为等腰三角形，则这样的点C的坐标为　 　．

    （﹣8，0）,（3，0）,（2，0）,（，0）． 【解析】当x=0时，y=4，当y=0时，x=﹣3，即A（﹣3，0），B（0，4）， ∴OA=3，OB=4， 由勾股定理得AB=5， 有三种情况：①以A为圆心，以AB为半径交x轴于两点，此时AC=AB=5，C的坐标是（2，0）和（﹣8，0）；②以B为圆心，以AB为半径交x轴于一点（A除外），此时AB=BC，OA=OC=3，C的...

    查看答案和解析>>

    科目：初中数学 来源：河南省郑州市郑东新区实验学校2017-2018学年八年级（上）期中数学试卷 题型：单选题

    在平面直角坐标系中，已知线段AB的两个端点分别是A（﹣4，﹣1），B（1，1），将线段AB平移得到线段A′B′，若点A′的坐标为（﹣2，2），则点B′的坐标为（　　）

    A. （3，4） B. （4，3） C. （﹣1，﹣2） D. （﹣2，﹣1）

    A 【解析】由题意可知A（﹣4，﹣1）的对应点A′的坐标为（﹣2，2 ），即可得坐标的变化规律为各对应点之间的关系是横坐标加2，纵坐标加3，由此可得点B′的横坐标为1+2=3，纵坐标为1+3=4，所以点B′的坐标为（3，4）．故选A．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级上册 第十三章 轴对称 13.1 轴对称 同步练习题 题型：填空题

    我国传统的木房屋窗子常用各种图案装饰,如图是一种常见图案,这个图案有____条对称轴.

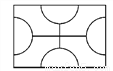
    2 【解析】试题分析：根据轴对称图形的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形． 这是一个组合图形，它的外部是一个长方形，再根据它的组合特点，显然有2条对称轴，即两组对边的垂直平分线． 故答案为2．

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型：单选题

    如图，从⊙O外一点P引⊙O的两条切线PA，PB，切点分别为A，B．如果∠APB=60°，PA=8，那么弦AB的长是（　　）

    A. 4 B. 8 C. 4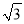 D. 8

    B 【解析】试题分析：∵PA,PB是圆O的两条切线，∴PA=PB. 又∵∠APB=60°，∴是等边三角形. 又∵PA=8，∴AB=8. 故选B.

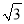
    查看答案和解析>>

    科目：初中数学 来源：山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型：解答题

    如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成正方形零件PQMN，使正方形PQMN的边QM在BC上，其余两个项点P，N分别在AB，AC上．求这个正方形零件PQMN面积S．

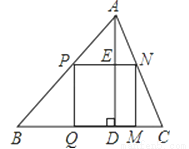
    正方形零件PQMN面积是2304mm2. 【解析】试题分析：PN与AD交于点E，如图，设MN=xmm，则AE=AD﹣ED=80﹣x，再证明△APN∽△ABC，利用相似比可表示出PN=（80﹣x），根据正方形的性质得到（80﹣x）=x，然后结合正方形的面积公式进行解答即可． 试题解析：PN与AD交于点E，如图，设MN=xmm， 易得四边形MNED为矩形，则ED=MN=x， ∴...

    查看答案和解析>>

    同步练习册答案