
我们知道,假分数可以化为带分数.例如: 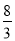 =2+
=2+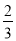 =2
=2 在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如: 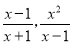 这样的分式就是假分式;
这样的分式就是假分式; 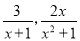 这样的分式就是真分式 .类似的,假分式也可以化为带分式(即:整式与真分式和的形式).
这样的分式就是真分式 .类似的,假分式也可以化为带分式(即:整式与真分式和的形式).
例如: 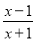 =
=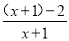 =1-
=1-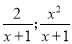 =
=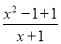 =
=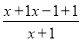 =
= 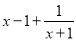

(1)将分式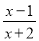 化为带分式;
化为带分式;
(2)若分式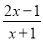 的值为整数,求x的整数值.
的值为整数,求x的整数值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:江苏省南通市崇川区2015-2016学年八年级上学期期末考试数学试卷 题型:解答题
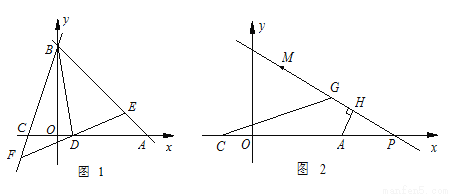
如图1,已知A(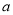 ,0),B(0,
,0),B(0, 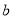 )分别为两坐标轴上的点,且
)分别为两坐标轴上的点,且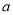 、
、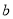 满足
满足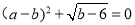 ,OC∶OA=1∶3.
,OC∶OA=1∶3.
(1)求A、B、C三点的坐标;
(2)若D(1,0),过点D的直线分别交AB、BC于E、F两点,设E、F两点的横坐标分别为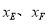 .当BD平分△BEF的面积时,求
.当BD平分△BEF的面积时,求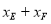 的值;
的值;
(3)如图2,若M(2,4),点P是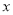 轴上A点右侧一动点,AH⊥PM于点H,在HM上取点G,使HG=HA,连接CG,当点P在点A右侧运动时,∠CGM的度数是否改变?若不变,请求其值;若改变,请说明理由.
轴上A点右侧一动点,AH⊥PM于点H,在HM上取点G,使HG=HA,连接CG,当点P在点A右侧运动时,∠CGM的度数是否改变?若不变,请求其值;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源:江苏省南通市崇川区2015-2016学年八年级上学期期末考试数学试卷 题型:填空题
若分式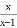 有意义,则x满足的条件是___________.
有意义,则x满足的条件是___________.
查看答案和解析>>
科目:初中数学 来源:江苏省南通市崇川区2015-2016学年八年级上学期期末考试数学试卷 题型:单选题
下面式子从左边到右边的变形是因式分解的是( )
A. 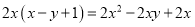 B.
B. 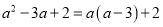
C. 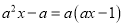 D.
D. 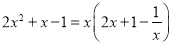
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷及答案 题型:解答题
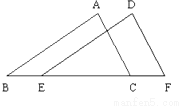
如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件:
①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷及答案 题型:填空题
已知, 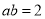 ,
, 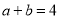 ,则式子
,则式子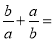 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷及答案 题型:单选题
在下列四个图案中,是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:山东省淄博市2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
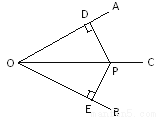
如图, 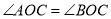 ,点
,点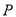 在
在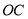 上,
上, 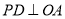 于点
于点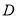 ,
, 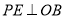 于点
于点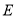 ,若
,若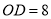 ,
, 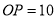 ,则
,则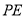 的长为( )
的长为( )
A. 5 B. 6 C. 7 D. 8
B 【解析】由PD⊥OA,可得∠PDO=90°,在Rt△ODP中,OD=8,OP=10,根据勾股定理求得PD=6,又因∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,根据角平分线的性质定理可得PE=PD=6.故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com