练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

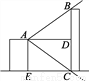
    如图，某人在楼顶A点处看到一烟囱顶端B的仰角∠BAD＝42°，看到烟囱底部C的俯角∠CAD也是42°，如果楼AE高是15米，那么烟囱BC高__米．

    30 【解析】∵∠BAD=∠CAD=42°， ∴AD是∠BAC的平分线. ∵AD⊥BC， ∴BD=CD. ∴BC=2CD=2AE=30. 故烟囱的高度为30米.故答案为:30.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级下册第三章3.1用表格表示的变量间关系课时练习 题型：单选题

    如果用总长为60m的篱笆围成一个长方形场地，设长方形的面积为S（m2），周长为p（m），一边长为a（m），那么S，p，a中是变量的是（　　）

    A. S和p B. S和a C. p和a D. S，p，a

    B 【解析】∵篱笆的总长为60米， ∴周长P是定值，而面积S和一边长a是变量， 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：解答题

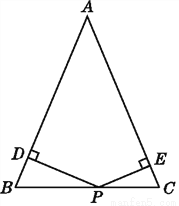
    如图,已知在△ABC中,AB=AC=4,P是BC边上任一点,PD⊥AB,PE⊥AC,D,E为垂足.若△ABC的面积为6,问:PD+PE的值能否确定?若能确定,值是多少?请说明理由.

    PD+PE的值能确定,且PD+PE=3 【解析】试题分析：可连接AP，由图得，S△ABC=S△ABP+S△ACP，代入数值，求解即可． 试题解析：【解析】 PD+PE的值能确定，且PD+PE=3．理由如下： 如图，连接AP． 由图可得S△ABC=S△ABP+S△ACP． 因为PD⊥AB，PE⊥AC，AB=AC=4，△ABC的面积为6， 所以6=×4×PD+×4...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：单选题

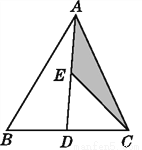
    如图,在△ABC中,D,E分别为BC,AD的中点,且S△ABC=4,则S阴影为(　　)

    A. 2 B. 1 C. 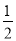D.

    B 【解析】【解析】 ∵D、E分别为BC，AD的中点，且S△ABC=4，∴S阴影=×S△ADC=×S△ABC=×4=1．故选B．

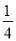
    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型：填空题

    某大学计划为新生配备如图①所示的折叠凳，图②是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计)，其中凳腿AB和CD的长相等，O是它们的中点，为了使折叠凳坐着舒适，厂家将撑开后的折叠凳宽度AD设计为30cm，则由以上信息可推得CB的长度为_____.

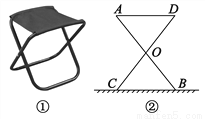
    30cm 【解析】∵O是AB、CD的中点， ∴OA=OB，OC=OD， 在△AOD和△BOC中， ， ∴△AOD≌△BOC(SAS)， ∴CB=AD， ∵AD=30cm， ∴CB=30cm. 故答案为：30cm.

    查看答案和解析>>

    科目：初中数学 来源：内蒙古包头市青山区2017-2018学年八年级（上）期末数学试卷 题型：解答题

    如图，已知直线AB∥CD，∠A=∠C=100°，E，F在CD上，且满足∠DBF=∠ABD，BE平分∠CBF．

    （1）求证：AD∥BC；

    （2）求∠DBE的度数；

    （3）若平行移动AD，在平行移动AD的过程中，是否存在某种情况，使∠BEC=∠ADB？若存在，求出其度数；若不存在，请说明理由．

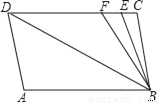
    （1）证明见解析；（2）40°；（3）60°. 【解析】试题分析：（1）根据平行线的性质，以及等量代换证明∠ADC+∠C=180°，即可证得AD∥BC； （2）由直线AB∥CD，根据两直线平行，同旁内角互补，即可求得∠ABC的度数，又由∠DBE=∠ABC，即可求得∠DBE的度数． （3）首先设∠ABD=∠DBF=∠BDC=x°，由直线AB∥CD，根据两直线平行，同旁内角互补与两直...

    查看答案和解析>>

    科目：初中数学 来源：内蒙古包头市青山区2017-2018学年八年级（上）期末数学试卷 题型：填空题

    小明想知道学校旗杆有多高，他发现旗杆上的绳子垂到地面还余1m，当他把绳子下端拉开5m后，发现下端刚好接触地面，则旗杆高度为_____米．

    12 【解析】根据题意，构建数学模型为： 设绳子长AC=x，则旗杆的高为AB=x-1，而绳子拉开的距离：BC=5，根据勾股定理可得，解得x=13，所以旗杆的高度AB=12米. 故答案为：12.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下5.3.1 等腰三角形的性质 同步练习 题型：单选题

    如图,已知四个图形分别是等边三角形、等腰梯形、正方形、圆,它们全是轴对称图形,其中对称轴的条数最少的图形是(　　)

    A.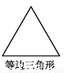

    B.

    C.

    D.

    B 【解析】试题解析： A. 等边三角形有3条对称轴，为三条高线所在的直线； B. 等腰梯形有1条对称轴，是过两底边中点的直线； C. 正方形有4条对称轴，为过对边中点的直线与两对角线所在的直线； D. 圆有无数条对称轴，为过圆心的直线. 故对称轴的条数最少的图形是等腰梯形. 故选B.

    查看答案和解析>>

    同步练习册答案