
��ͼ,��֪�ĸ�ͼ�ηֱ��ǵȱ������Ρ��������Ρ������Ρ�Բ,����ȫ����Գ�ͼ��,���жԳ�����������ٵ�ͼ����(����)
A. 
B. 
C. 
D. 

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ����ʦ������꼶�²� ������ ������ 4.5 ����������ȫ�Ȳ���� ͬ������ ���ͣ������
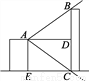
��ͼ��ij����¥��A�㴦����һ�̴Ѷ���B�����ǡ�BAD��42�㣬�����̴ѵײ�C�ĸ��ǡ�CADҲ��42�㣬���¥AE����15�ף���ô�̴�BC��__�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
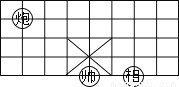
��ͼ���������̵�һ���֣�����˧��λ�ڵ㣨2����1���ϣ����ࡱλ�ڵ㣨4����1���ϣ����ڡ����ڵĵ��������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��5.3.1 ���������ε����� ͬ����ϰ ���ͣ������
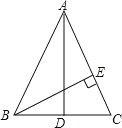
��ͼ���ڡ�ABC�У�AB=AC��AD��BC���ϵ����ߣ�BE��AC�ڵ�E����֤����CBE=��BAD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��5.3.1 ���������ε����� ͬ����ϰ ���ͣ���ѡ��
��ͼ������������ABC�У�AB=AC��BDƽ�֡�ABC����A=36�㣬���1�Ķ���Ϊ��������
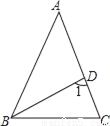
A. 36�� B. 60�� C. 72�� D. 108��
C �����������ݡ�A=36�㣬AB=AC�����ABC�Ķ��������ݽ�ƽ���ߵĶ��������ABD�Ķ��������������ε���ǵ����ʼ���õ��𰸣� �������� �ߡ�A=36�㣬AB=AC�����ABC=��C=72�㣬��BDƽ�֡�ABC�����ABD=36�㣬���1=��A+��ABD=72�㣬 ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018 ��ʦ������꼶��ѧ�²� �����¡�����֮��Ĺ�ϵ ��Ԫ���Ծ� ���ͣ������
ij����������ǰ����������42L.��ʻ����Сʱ��;���ڼ���վ������������������������Q(L)����ʻʱ��t(h)֮��Ĺ�ϵ��ͼ��ʾ������ͼ��ش����⣮
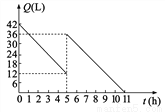
(1)��������ʻ��Сʱ����ͣ�
(2)��;����________L��
(3)�������վ��Ŀ�ĵػ���240km������Ϊ40km/h��Ҫ����Ŀ�ĵأ������е����Ƿ��ã���˵��ԭ��
(1)5Сʱ(2)24(3)�����е��պù��ã� �������������������1������ͼ��ɵã�5Сʱʱ���������ڵ��ʹ�12����Ϊ��36������5Сʱ����ͣ� ��2����36-12���ɣ� ��3�����ȼ�������������ٸ���·�̺��ٶȼ������ʻ240km��ʱ�䣬Ȼ����ʱ����Ժ������ɵ������ĵ��ͣ�����������������бȽϼ��ɣ� ���������(1)����ͼ���ֱ�ӵõ�����������ʻ5Сʱ����ͣ� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018 ��ʦ������꼶��ѧ�²� �����¡�����֮��Ĺ�ϵ ��Ԫ���Ծ� ���ͣ������
ij�ִ������������0.2%������100Ԫ������۳���Ϣ˰����Ϣ��y(Ԫ)����������x(xΪ������)֮��Ĺ�ϵΪ__________,4���µı�Ϣ��Ϊ________.
y��100��0.2x 100.8Ԫ ����������һ����y=100+100��0.2�G�� �ڶ�����y=100+100��0.2�G+��100+100��0.2�G����0.2�G �����ɿ�֪y=100(1+0.2�Gx)= y��100��0.2x�� ��x=4,���y=100.8. �ʴ�Ϊ�� y��100��0.2x��100.8Ԫ.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��4.3.2 �á��DZ߽ǡ��ǽDZߡ��ж�������ȫ�� ͬ����ϰ ���ͣ������
��ͼ��,�ڡ�ABC��,��ACB=90��,AC=BC,����C�ڡ�ABC����ֱ��MN,AM��MN�ڵ�M,BN��MN�ڵ�N.
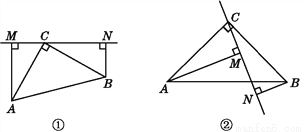
(1)��˵��:MN=AM+BN.
(2)��ͼ��,������C��ֱ��MN���߶�AB�ཻ,AM��MN�ڵ�M,BN��MN�ڵ�N(AM>BN),(1)�еĽ����Ƿ���Ȼ����?˵������.
(1) �𰸼�����;(2) ������ �������������������1�����û����ϵ֤����MAC=��NCB���֡�AMC=��CNB=90�㣬AC=BC���ʿ�֤��AMC�ա�CNB���Ӷ���AM=CN��MC=BN�����ɵó����ۣ� ��2�������ڣ�1���ķ�����֤����AMC�ա�CNB���Ӷ���AM=CN��MC=BN�����Ƴ�AM��BN��MN֮���������ϵ�� ����������⣺��1����AM��MN��BN��MN�����A...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ�²����� �ڶ��� �ཻ����ƽ���� ���ͣ������
��һ�����ǰ�ƴ����ͼ��ʾ��ͼ�Σ�����C��CFƽ�֡�DCE��DE�ڵ�F��
��1����֤��CF��AB��
��2�����DFC�Ķ�����
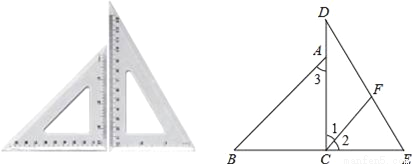
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com