
从﹣3,﹣2,﹣1,0,1,2,3这七个数中随机抽取一个数记为a,则a的值是不等式组 的解,但不是方程x2﹣3x+2=0的实数解的概率为_____.
的解,但不是方程x2﹣3x+2=0的实数解的概率为_____.
科目:初中数学 来源:广东省河源市和平县2017-2018学年七年级(上)期中数学试卷(解析版) 题型:解答题
计算:(1)12﹣(﹣18)+(﹣12)﹣15;(2)(﹣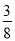 +
+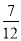 )×(﹣24)
)×(﹣24)
(3)(﹣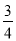 )×1
)×1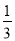 ÷(﹣1
÷(﹣1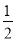 );(4)(﹣2)3×(﹣
);(4)(﹣2)3×(﹣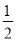 )﹣(﹣3)
)﹣(﹣3)
查看答案和解析>>
科目:初中数学 来源:广东省河源市和平县2017-2018学年七年级(上)期中数学试卷(解析版) 题型:单选题
下列各组式子中是同类项的是( )
A. 4x与﹣4y B. 4y与﹣4xy C. 4xy2与﹣4x2y D. ﹣4xy2与4y2x
D 【解析】试题分析:如果两个单项式,它们所含的字母相同,并且相同字母的指数也分别相同,那么就称这两个单项式为同类项.A选项字母不相同,不是同类项;B选项字母不相同,不是同类项;C选项相同字母的指数不相同,不是同类项;D选项是同类项,故选D.查看答案和解析>>
科目:初中数学 来源:2017年重庆市中考数学模拟试卷 题型:解答题
已知反比例函数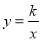 的图象经过点A(1,3).
的图象经过点A(1,3).
(1)试确定此反比例函数的解析式;
(2)当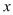 =2时, 求y的值;
=2时, 求y的值;
(3)当自变量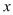 从5增大到8时,函数值y是怎样变化的?
从5增大到8时,函数值y是怎样变化的?
查看答案和解析>>
科目:初中数学 来源:2017年重庆市中考数学模拟试卷 题型:单选题
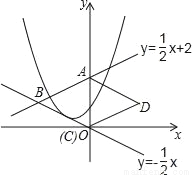
如图,直线y=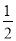 x+2与y轴交于点A,与直线y=﹣
x+2与y轴交于点A,与直线y=﹣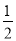 x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣
x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣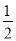 x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
A. ﹣2≤h≤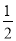 B. ﹣2≤h≤1 C. ﹣1≤h≤
B. ﹣2≤h≤1 C. ﹣1≤h≤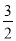 D. ﹣1≤h≤
D. ﹣1≤h≤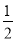
查看答案和解析>>
科目:初中数学 来源:2017年重庆市中考数学模拟试卷 题型:单选题
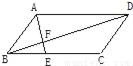
如图,F是平行四边形ABCD对角线BD上的点,BF:FD=1:3,则BE:EC=( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市2017-2018学年七年级12月月考数学试卷 题型:填空题
武汉开发区一初中官士墩校区前期建设投入约153000000元.数据153000000用科学记数法可表示为_________________ .
1.53×108 【解析】【解析】 153000000=1.53×108.故答案为:1.53×108.查看答案和解析>>
科目:初中数学 来源:重庆市2017-2018学年七年级上学期第三次月考数学试卷(答案不全) 题型:解答题
某同学在计算一个多项式减去﹣a2﹣2a+1时,因误看做加上﹣a2﹣2a+1,得到的答案3a2﹣2a+4,你能帮助这个同学做出正确答案吗?请写出解答过程.
5a2+2a+2. 【解析】分析:设该整式为A,由该整式加上-a²-2a+1,得到3a²-2a+4求出A,进而得到正确答案. 本题解析:设该整式为A,∵该整式加上﹣a2﹣2a+1,得到3a2﹣2a+4, ∴A=3a2﹣2a+4﹣(﹣a2﹣2a+1)=3a2﹣2a+4+a2+2a﹣1=4a2+3, ∴正确答案为:4a2+3﹣(﹣a2﹣2a+1)=4a2+3+a2+2a﹣1=5...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com