练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

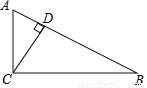
    已知CD是Rt△ABC斜边上的高线，且AB=10，若BC=8，则cos∠ACD= ______ ．

    【解析】试题分析：根据同角的余角相等得：∠ACD=∠B，利用同角的余弦得结论． 【解析】 ∵CD是Rt△ABC斜边上的高线， ∴CD⊥AB， ∴∠A+∠ACD=90°， ∵∠ACB=90°， ∴∠B+∠A=90°， ∴∠ACD=∠B， ∴cos∠ACD=cos∠B===， 故答案为： .
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型：单选题

    三角形的三个内角( )

    A、至少有两个锐角 B、至少有一个直角

    C、至多有两个钝角 D、至少有一个钝角

    A 【解析】根据三角形的内角和是180°判断即可． 【解析】 根据三角形的内角和是180°，知：三个内角可以都是60°，排除B； 三个内角可以都是锐角，排除C和D； 三角形的三个内角中至少有两个锐角，不可能有两个钝角或两个直角． 故选A． 考查了三角形的内角和定理：三角形的三个内角和是180°．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册 22.3 二次函数的应用 同步测试 题型：解答题

    为解决消费者停车难的问题，某商场新建一小型轿车停车场，经测算，此停车场每天需固定支出的费用（包括设施维修费、管理人员工资等）为600元，为制定合理的收费标准，该商场对每天轿车停放辆次（每辆轿车每停放一次简称为“辆次”）与每辆轿车的收费情况进行调查，发现每辆次轿车的停车费定价不超过10元时，每天来此停放的轿车都为300辆次；若每辆次轿车的停车费定价超过10元，则每超过1元，每天来此停放的轿车就减少12辆次，设每辆次轿车的停车费x元（为便于结算，停车费x只取整数），此停车场的日净收入为y元（日净收入=每天共收停车费﹣每天固定的支出）回答下列问题：

    （1）①当x≤10时，y与x的关系式为： ；

    ②当x＞10时，y与x的关系式为： ；

    （2）停车场能否实现3000元的日净收入？如能实现，求出每辆次轿车的停车费定价，如不能实现，请说明理由；

    （3）该商场要求此停车场既要吸引顾客，使每天轿车停放的辆次较多，又要有最大的日净收入，按此要求，每辆次轿车的停车费定价应定为多少元？此时最大日净收入是多少元？

    （1）①y=300x﹣600；②y=﹣12x2+420x﹣600；（2）停车场能实现3000元的日净收入，每辆次轿车的停车费定价是15元或20元；（3）每辆次轿车的停车费定价应定为17元，此时最大日净收入是3072元． 【解析】试题分析：(1)、①、当x≤10时，总费用=300×单价-工资得出答案；②、x＞10时，停车的数量为：300-12(x-10)，然后根据总费用=定价×数量-工资得出函...

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市2018届九年级上学期期中考试数学试卷 题型：解答题

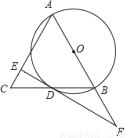
    如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．

    （1）判断直线DE与⊙O的位置关系，并说明理由；

    （2）如果AB=5，BC=6，求DE的长．

    （1）相切，理由见解析；（2）DE=． 【解析】试题分析：（1）连接AD，OD，根据已知条件证得OD⊥DE即可； （2）根据勾股定理计算即可． 【解析】 （1）相切， 理由如下： 连接AD，OD， ∵AB为⊙O的直径， ∴∠ADB=90°． ∴AD⊥BC． ∵AB=AC， ∴CD=BD=BC． ∵OA=OB， ∴OD∥AC．...

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市2018届九年级上学期期中考试数学试卷 题型：解答题

    计算：（1）sin260°+cos260°-tan45°； （2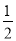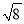）|-|+-4cos45°+2sin30°．

    （1）原式=0；（2）原式=． 【解析】试题分析：利用特殊角的锐角三角形函数值即可求解. 【解析】 （1）原式=+-1=1-1=0； （2）原式=

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市2018届九年级上学期期中考试数学试卷 题型：单选题

    如图，△ABC中，P为AB上一点，在下列四个条件中，①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP·AB；④AB·CP=AP·CB，其中能满足△APC和△ACB相似的条件是( )

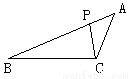
    A、①②④ B、①③④    C、②③④ D、①②③

    D 【解析】 试题分析：由图可得△APC和△ACB已经有一个公共角∠A，再根据相似三角形的判定方法依次分析各小题即可判断. ①∠ACP=∠B，②∠APC=∠ACB，③即，能满足； ④即，夹角应为∠B，故不能满足； 故选D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习（含解析） 题型：解答题

    一份试卷，一共30道选择题，答对一题得3分，答错一题扣1分，小红每题都答了，共得78分，那么小红答对了几道题？请根据题意，列出方程．

    3x－（30－x）×1＝78． 【解析】等量关系为:答题得分=答对的题得分－答错题扣的分,设答对了x道题,则答错了(30－x)道题,答对题得分为:3x,答错的题扣分为: (30－x),根据题意可列出方程. 试题解析:设小红答对了x道题,由题意得: 3x－（30－x）×1＝78.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习（含解析） 题型：单选题

    希望中学九年级1班共有学生49人，当该班少一名男生时，男生的人数恰好为女生人数的一半．设该班有男生x人，则下列方程中，正确的是（ ）

    A. 2（x－1）＋x＝49

    B. 2（x＋1）＋x＝49

    C. x－1＋2x＝49

    D. x＋1＋2x＝49

    A 【解析】试题分析：利用该班少一名男生时，男生人数恰为女生人数的一半用男生的人数表示出女生的人数，利用女生人数+男生人数=49求解． 【解析】 设男生人数为x人，则女生为2（x﹣1）， 根据题意得：2（x﹣1）+x=49， 故选A．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.3实际问题与二次函数（3）测试 题型：解答题

    如图4所示，一座抛物线型拱桥，桥下水面宽度是4m，拱高是2m，当水面下降1m后，水面宽度是多少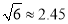？（，结果保留0.1m）

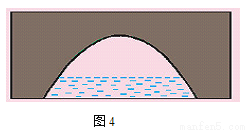
    4.9 【解析】试题分析：首先以水面的水平线为x轴，抛物线两端点中点为原点设立平面直角坐标系，设函数解析式为： ，将(0，2)和(2，0)代入求出函数解析式，最后将y=-1代入函数解析式求出x的值，从而的得出水面的宽度． 试题解析：设水面的水平线为x轴，抛物线两端点中点为原点设立平面直角坐标系， 设抛物线的函数关系式为： ， 因为抛物线过点（0，2）， 所以有， 又因为抛物...

    查看答案和解析>>

    同步练习册答案