练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图4所示，一座抛物线型拱桥，桥下水面宽度是4m，拱高是2m，当水面下降1m后，水面宽度是多少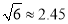？（，结果保留0.1m）

    4.9 【解析】试题分析：首先以水面的水平线为x轴，抛物线两端点中点为原点设立平面直角坐标系，设函数解析式为： ，将(0，2)和(2，0)代入求出函数解析式，最后将y=-1代入函数解析式求出x的值，从而的得出水面的宽度． 试题解析：设水面的水平线为x轴，抛物线两端点中点为原点设立平面直角坐标系， 设抛物线的函数关系式为： ， 因为抛物线过点（0，2）， 所以有， 又因为抛物...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省聊城市2018届九年级上学期期中考试数学试卷 题型：填空题

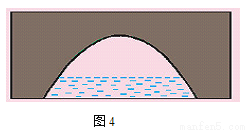
    已知CD是Rt△ABC斜边上的高线，且AB=10，若BC=8，则cos∠ACD= ______ ．

    【解析】试题分析：根据同角的余角相等得：∠ACD=∠B，利用同角的余弦得结论． 【解析】 ∵CD是Rt△ABC斜边上的高线， ∴CD⊥AB， ∴∠A+∠ACD=90°， ∵∠ACB=90°， ∴∠B+∠A=90°， ∴∠ACD=∠B， ∴cos∠ACD=cos∠B===， 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 第23章小结与复习 测试 题型：填空题

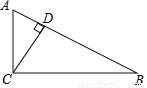
    如图，在平面直角坐标系中， 若△ABC与△A1B1C1关于E点成中心对称， 则对称中心E点的坐标是 ．

    （3，-1） 【解析】 试题分析：连接对应点AA1、CC1，根据对应点的连线经过对称中心，则交点就是对称中心E点，在坐标系内确定出其坐标． 试题解析：如图： 连接AA1、CC1，则交点就是对称中心E点．观察图形知，E（3，-1）．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级数学上册 第23章 旋转 同步单元检测试卷（Word版附答案） 题型：单选题

    如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：

    ①AC=AD；②BD⊥AC；③四边形ACED是菱形．

    其中正确的个数是（ ）

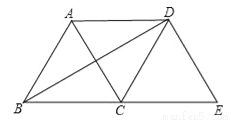
    A．0 B．1 C．2 D．3

    D． 【解析】试题分析：根据旋转和等边三角形的性质得出∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，求出△ACD是等边三角形，求出AD=AC，根据菱形的判定得出四边形ABCD和ACED都是菱形，根据菱形的判定推出AC⊥BD． ∵将等边△ABC绕点C顺时针旋转120°得到△EDC， ∴∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE， ∴∠ACD...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.3实际问题与二次函数（3）测试 题型：解答题

    花香村计划改造一片林地，估计这片林地可种梨树80~133棵.根据经验，若种100棵树，果树成熟后平均每棵树上能结500个梨，在这个基础上每多种一棵梨树，平均每棵会少结3个梨，每少种一棵，平均每棵树会多结4个梨.

    （1）如果种植110棵梨树，则总共能结多少个梨？

    （2）设种植x棵梨树，总共能结y个梨，

    ①当80≤x≤100时，求出y与x之间的函数关系式；

    ②当100<x≤134时，求出y与x之间的函数关系式；

    （3）种多少棵梨树，总共能结的梨数最多？最多是多少？

    （1）51700（2）①② (3)当x=133时，有最大值，最大值是53333个梨 【解析】试题分析：(1)、根据题意首先得出每棵树上能结多少果实，然后求出总量；(2)、当80≤x≤100时，平均每棵树上能结[500+4（100-x）]个梨，然后得出函数解析式；当100

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.3实际问题与二次函数（3）测试 题型：填空题

    某纸箱厂第1年的利润为50万元，如果每一年比上一年的利润增长率相同，都是x，则第3年的利润为____万元。

    50（1+x）2 【解析】试题分析：根据题意可知：第2年的利润为：50(1+x)万元，第3年的利润为：50(1+x)(1+x)= 万元．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.3实际问题与二次函数（3）测试 题型：单选题

    抛物线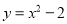的顶点坐标为（ ）

    A. （2，0） B. （-2，0） C. （0，2） D. （0，-2）

    D 【解析】试题分析：对于二次函数的顶点坐标为(0，b)，根据题意可知二次函数的顶点坐标为(0，-2)，故选择D．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年人教八年级数学上册 第14章 章末综合检测 题型：单选题

    下列等式成立的是（ ）

    A. （-a-b）2+（a-b）2=-4ab B. （-a-b）2+（a-b）2=a2+b2

    C. （-a-b）（a-b）=（a-b）2 D. （-a-b）（a-b）=b2-a2

    【答案】D

    【解析】解析：∵（-a-b）2+（a-b）2=（a+b）2+（a-b）2=（a2+2ab+b2）+（a2-2ab+b2）=2a2+2b2，

    ∴选项A与选项B错误；

    ∵（-a-b）（a-b）=-（a+b）（a-b）=-（a2-b2）=b2-a2，∴选项C错误，选项D正确.

    故选D.

    【题型】单选题
    【结束】
    8

    若x=1，y=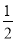，则x2+4xy+4y2的值是（ ）

    A. 2 B. 4 C. 32 D. 12

    B 【解析】解析：x2+4xy+4y2=（x+2y）2==4.故选B.

    查看答案和解析>>

    科目：初中数学 来源：人教版数学八年级上册 第11章 11.3.1 多边形同步练习（解析版） 题型：单选题

    若凸n边形的每个外角都是36°，则从一个顶点出发引的对角线条数是（   ）

    A. 6 B. 7 C. 8 D. 9

    B 【解析】360°÷36°=10， 10?3=7. 故从一个顶点出发引的对角线条数是7. 故选：B.

    查看答案和解析>>

    同步练习册答案