
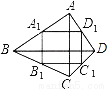
��ͼ���ı���ABCD�������Խ���AC��BD���ഹֱ��A1 �� B1 �� C1 �� D1���ı���ABCD���е��ı��Σ����AC=8��BD=10����ô�ı���A1B1C1D1�����Ϊ________��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰�16.2���θ�ʽ����ij˳�ͬ����ϰ ���ͣ������
��ʽ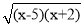 =
=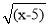 •
•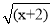 һ��������
һ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²���ѧ������Բ��Ԫ���� ���ͣ������
��ͼ,��֪A��B��C��D��E���ڡ�O��,��ACΪ��O��ֱ��,���A+��B+��C=________��.
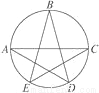
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²���ѧ������Բ��Ԫ���� ���ͣ���ѡ��
��ͼ����֪ԲO��ֱ��Ϊ6��CDΪԲO��ֱ������CD��AB����D=15�㣮��OE�ij�Ϊ��������
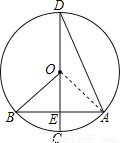
A. 3 B. 3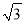 C.
C. 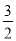 D.
D. 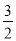
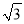
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧȫ���ۺϲ��Ծ� ���ͣ������
Ԫ�����ᣬ���ȫ��ѧ�������ļ���ˮ�����˵��飬Ϊ��ȷ����ʲôˮ������ֵ�ù�ע��Ӧ����ͳ�Ƶ������ݵ�________ �����λ��������ƽ����������������
���� ��������������������������������г��ִ������������ʰ��ֵ�ù�ע��Ӧ����ͳ�Ƶ������ݵ������� �ʴ�Ϊ���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧȫ���ۺϲ��Ծ� ���ͣ���ѡ��
��ͼ��������ABCD�У�AD��BC���Խ���BD����λ��EF���ڵ�O����FO-EO=3����BC-AD���� ( )

A.4�� B. 6�� C. 8�� D. 10.
B �������� ���������AD��BC��EFΪ������λ�ߣ�����EFͬ��ƽ�֣�BD��EOΪ��ABD��λ�ߣ�OFΪ��DBC��λ�ߡ� ����֪EO=AD��FO=BC��FO-EO=BC-AD=(BC-AD)=3,��BC-AD=6�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧȫ���ۺϲ��Ծ� ���ͣ���ѡ��
���ξ��ж�ƽ���ı��β�һ�����е������ǣ�������
A. �Խ���� B. �Ա����
C. �Խ������ D. �Խ�����ƽ��
C ��������������������ε� �Խ�����ȣ���ƽ���ı��εĶԽ��߲�һ�����. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰� 2018�괺 ���꼶��ѧ�²� ������ �ཻ����ƽ���� ����֤���� ���ͣ������
��ͼ,BE��AO,��1=��2,OE��OA�ڵ�O,EH��CO�ڵ�H,��ô��5=��6,Ϊʲô��
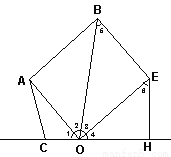
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²���ѧȫ���ۺϲ��Ծ� ���ͣ������
���4a2����x+y��2��1��9b2�У���ѡ��ʽ����õ���һ��ʽ�ӽ�����ʽ�ֽ���________
4a2��1=��2a��1����2a+1�� ������������ƽ���ʽ���ã� 4a2-1=��2a��2-12=��2a-1����2a+1���� �ʴ�Ϊ��4a2-1=��2a-1����2a+1�����𰸲�Ψһ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com