
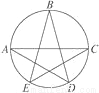
如图,已知A、B、C、D、E均在⊙O上,且AC为⊙O的直径,则∠A+∠B+∠C=________度.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第4章 一次函数 单元测试卷 题型:单选题
为了鼓励节约用水,按以下规定收取水费:(1)每户每月用水量不超过20立方米,则每立方米水费1.8元;(2)若每户每月用水量超过20立方米,则超过部分每立方米水费3元.设某户一个月所交水费为y(元),用水量为x(立方米),则y与x的函数关系用图象表示为( )
A. 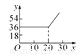 B.
B. 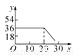 C.
C. 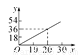 D.
D. 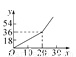
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2017-2018学年八年级上学期期中数学 题型:解答题
如图,将边长为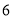 的正三角形纸片
的正三角形纸片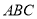 按如下顺序进行两次折叠,展开后,得折痕
按如下顺序进行两次折叠,展开后,得折痕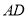 ,
, 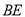 (如图①),点
(如图①),点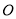 为其交点.
为其交点.
(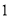 )探求
)探求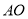 到
到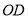 的数量关系,并说明理由.
的数量关系,并说明理由.
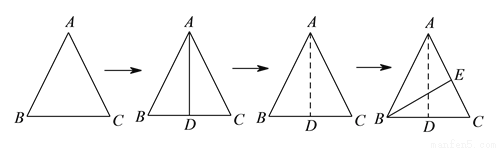
(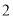 )如图②,若
)如图②,若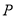 ,
, 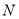 分别为
分别为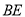 ,
, 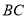 上的动点.
上的动点.
①当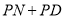 的长度取得最小值时,求
的长度取得最小值时,求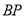 的长度.
的长度.
②如图③,若点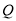 在线段
在线段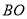 上,
上, 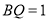 ,则
,则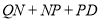 的最小值
的最小值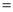 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2017-2018学年八年级上学期期中数学 题型:单选题
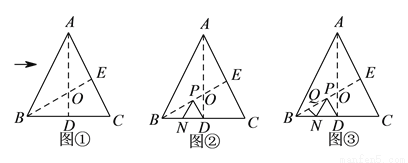
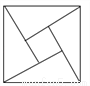
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若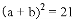 ,大正方形的面积为13,则小正方形的面积为( )
,大正方形的面积为13,则小正方形的面积为( )
A. 3 B. 4 C. 5 D. 6
C 【解析】试题分析:如图所示,∵,∴=21,∵大正方形的面积为13,2ab=21﹣13=8,∴小正方形的面积为13﹣8=5.故选C.查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:解答题
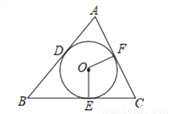
如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,S△ABC=10cm2,C△ABC=10cm且∠C=60°.求:
(1)⊙O的半径r;
(2)扇形OEF的面积(结果保留π);
(3)扇形OEF的周长(结果保留π)
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:填空题
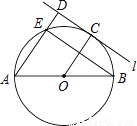
如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA=5,则线段DC的长为________.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:单选题
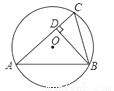
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则tan∠CBD的值等于( )
A. 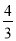 B.
B. 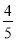 C.
C. 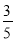 D.
D. 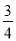
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:填空题
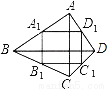
如图,四边形ABCD的两条对角线AC,BD互相垂直,A1 , B1 , C1 , D1是四边形ABCD的中点四边形,如果AC=8,BD=10,那么四边形A1B1C1D1的面积为________.
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册 第1-3章 综合测试卷 题型:填空题
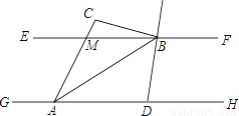
如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com