练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在梯形ABCD中，AD∥BC，对角线BD与中位线EF交于点O，若FO-EO=3，则BC-AD等于 ( )

    A.4； B. 6； C. 8； D. 10.

    B 【解析】 试题分析：AD∥BC且EF为梯形中位线，所以EF同样平分？BD，EO为△ABD中位线，OF为△DBC中位线。 ∴易知EO=AD，FO=BC。FO-EO=BC-AD=(BC-AD)=3,∴BC-AD=6
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年八年级数学人教版16.2二次根式定义的乘除同步练习 题型：单选题

    当x取某一范围的实数时，代数式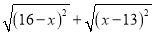的值是一个常数，该常数是（  ）

    A. 29 B. 16 C. 13 D. 3

    D 【解析】试题解析： (1)当时，解得：1316；原式=x?16+x?13=2x?29，不是常数； (4)当时，无解. 常数为3. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学第三章圆单元检测卷 题型：填空题

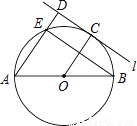
    如图，AB为⊙O的直径，直线l与⊙O相切于点C，AD⊥l，垂足为D，AD交⊙O于点E，连接OC、BE．若AE=6，OA=5，则线段DC的长为________．

    4 【解析】试题分析：令OC交BE于F，∵AB为⊙O的直径，∴∠AEB=90°，∵AD⊥CD，∴BE∥CD，∵CD为⊙O的切线，∴OC⊥CD，∴OC⊥BE，∴四边形CDEF为矩形，∴CD=EF，在Rt△ABE中，，∵OF⊥BE，∴BF=EF=4，∴CD=4．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学全册综合测试卷 题型：填空题

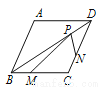
    如图，菱形ABCD的边长为6，M、N分别是边BC、CD的上点，且MC＝2MB，ND＝2NC．点P是对角线上BD上一点，则PM＋PN的最小值是_____．

    6 【解析】试题分析：作M关于BD的对称点Q，连接NQ，交BD于P，连接MP，此时MP+NP的值最小，连接AC，求出OC=AC=3、OB=BD=4，根据勾股定理求出BC=5，证出MP+NP=QN=BC=5．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学全册综合测试卷 题型：填空题

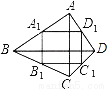
    如图，四边形ABCD的两条对角线AC，BD互相垂直，A1 ， B1 ， C1 ， D1是四边形ABCD的中点四边形，如果AC=8，BD=10，那么四边形A1B1C1D1的面积为________．

    20 【解析】试题解析：∵A1，B1，C1，D1是四边形ABCD的中点四边形，且AC=8，BD=10 ∴A1D1是△ABD的中位线 ∴A1D1=BD=×10=5 同理可得A1B1=AC=4 根据三角形的中位线定理，可以证明四边形A1B1C1D1是矩形 那么四边形A1B1C1D1的面积为A1D1×A1B1=5×4=20． 故答案为：20.

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学全册综合测试卷 题型：单选题

    下列条件中，不能判断四边形ABCD是平行四边形的是（   ）

    A. ∠A=∠C，∠B=∠D B. AB∥CD，AB=CD C. AB=CD，AD∥BC D. AB∥CD，AD∥BC

    C 【解析】试题解析：如图：、 A、∵∠A=∠C，∠B=∠D，∴四边形ABCD是平行四边形，正确，故本选项错误； B、∵AB∥CD，AB=CD，∴四边形ABCD是平行四边形，正确，故本选项错误； C、根据AB=CD，AD∥BC可能得出四边形是等腰梯形，不一定推出四边形ABCD是平行四边形，错误，故本选项正确； D、∵AB∥CD，AD∥BC，∴四边形ABCD是平行四边形...

    查看答案和解析>>

    科目：初中数学 来源：人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型：解答题

    如图,已知∠1=250,∠2=450, ∠3=300，∠4=100.求证:AB//CD.

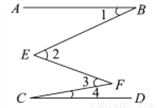
    证明见解析 【解析】试题分析：过点E作射线EM．使∠BEM=∠1=25°，过点F作射线FN，使∠EFN=20°，即可判断直线平行，再由平行线的性质和判定即可得到结论． 试题解析：证明：如图．过点E作射线EM．使∠BEM=∠1=25°， ∴AB//EM(内错角相等，两直线平行)． 又∠2=45°， ∴∠FEM= ∠2-∠BE=20°． 过点F作射线FN，使∠EFN...

    查看答案和解析>>

    科目：初中数学 来源：人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型：解答题

    如图，已知AD//BE,∠1=∠2.求证：∠A=∠E．

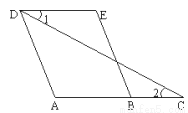
    证明见解析 【解析】试题分析：先根据平行线的性质得到∠A=∠EBC，再根据平行线的判定由∠1=∠2得到DE∥AC，则∠E=∠EBC，由此可以得到结论． 试题解析：证明：∵AD∥BE，∴∠A=∠EBC．∵∠1=∠2，∴DE∥AC，∴∠E=∠EBC， ∴∠A=∠E．

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学全册综合测试卷 题型：单选题

    如右图，在△ABC中，∠C=90°，AB的垂直平分线MN分别交AC，AB于点D，E． 若∠CBD : ∠DBA =3:1，则∠A为（ ）．

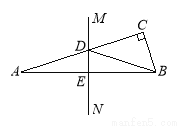
    A．18° B．20° C．22.5° D．30°

    A 【解析】∵MN垂直平分AB， ∴∠DBA=∠A， ∵∠CBD：∠DBA=3：1， ∴设∠DBA=x，则∠CBD=3x，∠A=x， ∴x+3x+x=90°， ∴x=18°， ∴∠A=18°

    查看答案和解析>>

    同步练习册答案