
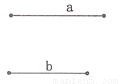
已知:如图,已知线段a、b,请你用直尺和圆规作一条线段,使它等于a+b. (要求:不写作法,保留痕迹,指出所求)
科目:初中数学 来源:北京市顺义区2017-2018学年度第一学期期末教学质量检测八年级数学试卷 题型:单选题
我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:
指数运算 | 21=2 | 22=4 | 23=8 | … | 31=3 | 32=9 | 33=27 | … |
新运算 | log22=1 | log24=2 | log28=3 | … | log33=1 | log39=2 | log327=3 | … |
根据上表规律,某同学写出了三个式子:
①log216=4,②log525=5,③log2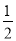 =﹣1.其中正确的是
=﹣1.其中正确的是
A. ①② B. ①③ C. ②③ D. ①②③
B 【解析】 ,故①正确; ,故②不正确; ,故③正确; 故选B.查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
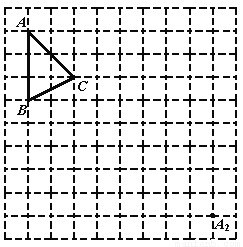
如图,是一个由边长为1的小正方形组成的10×10的正方形网格,
(1)在网格中画出将△ABC向右平移4个单位后的△A1B1C1;
(2)△ABC绕点O旋转180°后,点A与点A2重合,请在网格中画出点O,并画出△ABC绕点O旋转180°后的△A2B2C2;
(3)描述△A1B1C1与△A2B2C2的位置关系是 .
查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
将多项式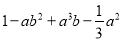 按字母a降幂排列是________________________.
按字母a降幂排列是________________________.
查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
在下列代数式中,是单项式的是( )
A. 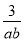 B.
B. 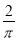 C.
C. 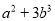 D.
D. 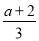
查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年七年级上学期期末测评数学试卷 题型:填空题
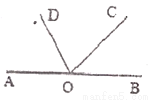
如图,点O是直线AB上的点,在AB同侧画射线OC、OD.且OD平分∠AOC.若∠BOC=57 ,则∠AOD=____
,则∠AOD=____
查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年七年级上学期期末测评数学试卷 题型:单选题
如图,∠BAC和∠DAE都是直角,∠BAE=108 ,则∠DAC的度数为( )
,则∠DAC的度数为( )
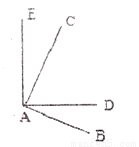
A. 36 B. 72
B. 72 C. 18
C. 18 D. 54
D. 54
查看答案和解析>>
科目:初中数学 来源:北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型:解答题
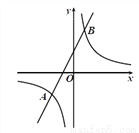
如图,在平面直角坐标系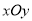 中,一次函数
中,一次函数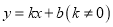 与反比例函数
与反比例函数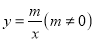 交于点
交于点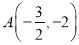 ,
, 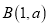 .
.
(1)分别求出反比例函数和一次函数的表达式;
(2)根据函数图象,直接写出不等式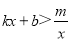 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
若代数式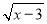 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
A. x≥-3 B. x>3 C. x≥3 D. x≤3
C 【解析】先根据二次根式有意义的条件列出关于x的不等式,求出x的取值范围即可. 【解析】 ∵代数式在实数范围内有意义, ∴x?3≥0, 解得x≥3. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com