
在下列代数式中,是单项式的是( )
A. 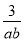 B.
B. 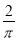 C.
C. 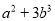 D.
D. 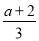
科目:初中数学 来源:北京市顺义区2017-2018学年度第一学期期末教学质量检测八年级数学试卷 题型:填空题
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为_____度.
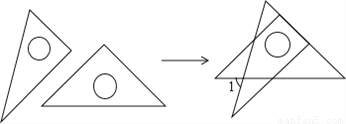
查看答案和解析>>
科目:初中数学 来源:北京市西城区2017-2018学年度第一学期期末考试七年级数学试卷 题型:单选题
如图所示,将两个圆柱体紧靠在一起,从上面看这两个立体图形,得到的平面图形是( ).
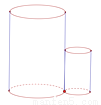
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
当x______时,分式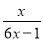 有意义..
有意义..
查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
下列说法中,正确的是( )
A. 将一个图形先向左平移3厘米,再向下平移5厘米,那么平移的距离是8厘米
B. 将一个图形绕任意一点旋转360°后,能与初始图形重合
C. 等边三角形至少旋转60°能与本身重合
D. 面积相等的两个三角形一定关于某条直线成轴对称
B 【解析】A.平移的距离是厘米,故不正确; B. 将一个图形绕任意一点旋转360°后,回到了原来的位置,所以能与初始图形重合,故正确; C. 等边三角形至少旋转120°能与本身重合,故不正确; D.面积相等的两个三角形不一定关于某条直线成轴对称,关于某条直线成轴对称两个三角形的面积一定相等,故不正确. 故选B.查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年七年级上学期期末测评数学试卷 题型:解答题
已知:如图,已知线段a、b,请你用直尺和圆规作一条线段,使它等于a+b. (要求:不写作法,保留痕迹,指出所求)
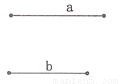
查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年七年级上学期期末测评数学试卷 题型:填空题
如图,要从B点到C点,有三条路线:①从B到A再到C;②从B到D再到C;③线段BC.要使距离最近,你选择路线____(填序号),理由是___________________
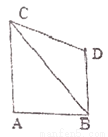
查看答案和解析>>
科目:初中数学 来源:北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型:解答题
如图1,在矩形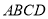 中,点
中,点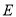 为
为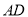 边中点,点
边中点,点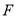 为
为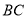 边中点;点
边中点;点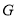 ,
, 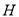 为
为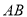 边三等分点,
边三等分点, 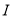 ,
, 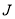 为
为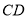 边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形
边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形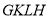 的面积与图3中四边形
的面积与图3中四边形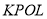 的面积相等吗?
的面积相等吗?
(1)小瑞的探究过程如下
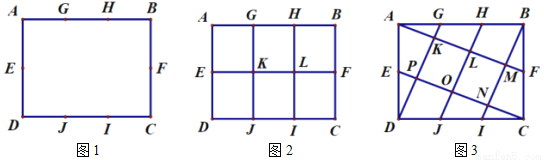
在图2中,小瑞发现,  ;
;
在图3中,小瑞对四边形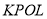 面积的探究如下. 请你将小瑞的思路填写完整:
面积的探究如下. 请你将小瑞的思路填写完整:
设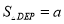 ,
, 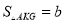
∵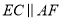
∴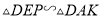 ,且相似比为
,且相似比为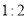 ,得到
,得到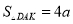
∵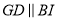
∴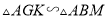 ,且相似比为
,且相似比为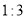 ,得到
,得到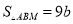
又∵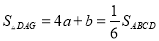 ,
, 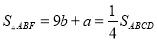
∴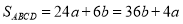
∴ ,
, 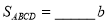 ,
, 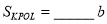
∴ ,则
,则 (填写“
(填写“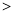 ”,“
”,“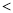 ”或“
”或“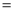 ”)
”)
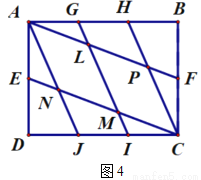
(2)小瑞又按照图4的方式连接矩形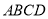 对边上的点.则
对边上的点.则 .
.
查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
如图,将△ABC沿DE翻折,折痕DE∥BC,若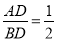 ,BC=9 ,则DE的长等于( )
,BC=9 ,则DE的长等于( )
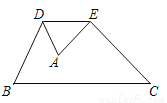
A. 2 B. 3 C. 4 D. 4.5
B 【解析】根据DE∥BC证得△DAE∽△BAC,可得,然后根据条件,BC=9即可求出DE的长. 【解析】 ∵DE∥BC, ∴△DAE∽△BAC, ∴, ∵, ∴, ∴, ∵BC=9, ∴DE=3. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com