练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，抛物线的表达式是( )

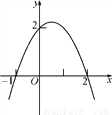
    A. y＝x2－x＋2

    B. y＝x2＋x＋2

    C. y＝－x2－x＋2

    D. y＝－x2＋x＋2

    D 【解析】解设y= , （）由图知 y= ,把（0,2）代入方程， 解得a=-1, y==,选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2018春季学北师大版九年级数学下册期末测评试卷 题型：解答题

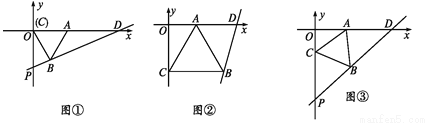
    △ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).

    (1)如图①,当点C与点O重合时,求直线BD的表达式;

    (2)如图②,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的☉B与y轴相切(切点为C)时,求点B的坐标;

    (3)如图③,点C从点O沿y轴向下移动,当点C的坐标为C(0,-2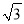)时,求∠ODB的正切值.

    （1）y=x-.（2）点B的坐标为(8,-4).（3）. 【解析】试题分析：（1）先根据等边三角形的性质求出B点的坐标，直接运用待定系数法就可以求出直线BD的解析式。 （2）作BE⊥x轴于E，就可以得出∠AEB=90°，由圆的切线的性质就可以而出B的纵坐标，由直角三角形的性质就可以求出B点的横坐标，从而得出结论。 （3）以点B为圆心，AB为半径作⊙B，交y轴于点C、E，过点B作B...

    查看答案和解析>>

    科目：初中数学 来源：宁夏2017-2018学年度上期七年级数学期末综合检测模拟试卷 题型：单选题

    如图所示的是由几个相同的小正方体搭成的一个几何体，从左面看到的图为(　　)

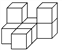
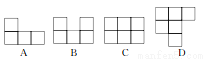
    A. （A） B. （B） C. （C） D. （D）

    A 【解析】试题解析：从左面看易得第一层有3个正方形，第二层最左边有一个正方形． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：吉林省2018届九年级（上）期中数学试卷 题型：填空题

    一次函数y=x+1与二次函数y=x2﹣x+2的图象有_____个交点．

    1 【解析】由 消去可得得方程： ，解得， ∴一次函数y=x+1与二次函数y=x2﹣x+2的图象有1个交点． 故答案为：1.

    查看答案和解析>>

    科目：初中数学 来源：吉林省2018届九年级（上）期中数学试卷 题型：单选题

    已知二次函数y=3（x+1）2﹣8的图象上有三点A（1，y1），B（2，y2），C（﹣2，y3），则y1，y2，y3的大小关系为（　　）

    A. y1＞y2＞y3 B. y2＞y1＞y3 C. y3＞y1＞y2 D. y3＞y2＞y1

    B 【解析】由二次函数y=3（x+1）2﹣8可知，其图象的对称轴为x=﹣1，开口向上， ∴ A（1，y1），B（2，y2），C（﹣2，y3）三点中，C点离对称轴最近，点B距离对称轴最远， ∴y2＞y1＞y3. 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017年四川省数学七年级（上）期末数学试卷 题型：解答题

    如图，直线AB与CD相交于点O，OF，OD分别是∠AOE，∠BOE的平分线.

    （1） 写出∠DOE的补角；

    （2）若∠BOE = 62°，求∠AOD和∠EOF的度数；

    （3）射线OD与OF之间的夹角是多少？

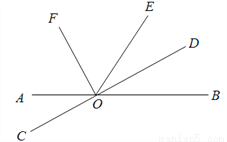
    （1）∠DOE的补角为∠COE，∠AOD，∠BOC；（2）∠AOD =149°，∠EOF = 59°；（3）∠DOF = 90° 【解析】试题分析：（1）根据互补的定义确定∠DOE的补角； （2）先根据角平分线的定义得出∠BOD的度数，再由邻补角定义可得∠AOD=180°-∠BOD；之后根据邻补角定义可得∠AOE=180°-∠BOE，再由角平分线的定义得出∠EOF的度数； （3）...

    查看答案和解析>>

    科目：初中数学 来源：2017年四川省数学七年级（上）期末数学试卷 题型：填空题

    当x=____________时，代数式4x－5的值等于－7.

    - 【解析】试题解析：4x-5=-7， 移项得：4x=-7+5， 合并同类项得：4x=-2， 把x的系数化为1得：x=-． 故答案为：-．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    如图，已知点C、F、E、B在一条直线上，CE=BF,DF = AE,∠CFD=∠BEA，写出CD与AB之间的关系，并证明你的结论.

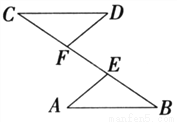
    CD=AB, CD∥AB,理由见解析 【解析】试题分析：求出CF=BE，根据SAS证△AEB≌△CFD，推出CD=AB，∠C=∠B，根据平行线的判定推出CD∥AB． 试题解析：结论：CD=AB, CD∥AB 证明：∵CE= B F FC－EF=FB－EF ∴CF= B E 在△ABC和△DEF中 ∴△CDF≌△BAE(SAS) ∴∠C＝∠B, CD=...

    查看答案和解析>>

    科目：初中数学 来源：贵州省2017-2018学年七年级（上）期中数学试卷 题型：单选题

    买一个足球需要m元，买一个篮球需要n元，则买4个足球、7个篮球共需要（　　）

    A. （7m+4n）元 B. 28mn元 C. （4m+7n）元 D. 11mn元

    C 【解析】∵4个足球需要4m元，7个篮球需要7n元， ∴买4个足球、7个篮球共需要（4m+7n）元， 故选：C．

    查看答案和解析>>

    同步练习册答案