练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

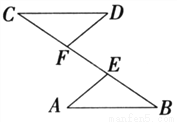
    如图，已知点C、F、E、B在一条直线上，CE=BF,DF = AE,∠CFD=∠BEA，写出CD与AB之间的关系，并证明你的结论.

    CD=AB, CD∥AB,理由见解析 【解析】试题分析：求出CF=BE，根据SAS证△AEB≌△CFD，推出CD=AB，∠C=∠B，根据平行线的判定推出CD∥AB． 试题解析：结论：CD=AB, CD∥AB 证明：∵CE= B F FC－EF=FB－EF ∴CF= B E 在△ABC和△DEF中 ∴△CDF≌△BAE(SAS) ∴∠C＝∠B, CD=...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：宁夏2017-2018学年度上期七年级数学期末综合检测模拟试卷 题型：解答题

    计算：（1）6÷( - 2)3 - | - 22×3| - 3÷2×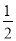+1；（2）-32+( - 4)×( - 5)×0.25 - 6÷.

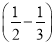    （1）原式=；（2）原式=-40 【解析】试题分析：（1）根据乘方、绝对值，有理数的乘除法进行计算即可； （2）根据运算顺序，进行计算即可. 试题解析：(1)原式=6÷( - 8) - 12 - +1 = - -12- +1 = (2)原式= - 9+5 – 36 = - 40.

    查看答案和解析>>

    科目：初中数学 来源：吉林省2018届九年级（上）期中数学试卷 题型：单选题

    如图，抛物线的表达式是( )

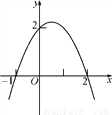
    A. y＝x2－x＋2

    B. y＝x2＋x＋2

    C. y＝－x2－x＋2

    D. y＝－x2＋x＋2

    D 【解析】解设y= , （）由图知 y= ,把（0,2）代入方程， 解得a=-1, y==,选D.

    查看答案和解析>>

    科目：初中数学 来源：2017年四川省数学七年级（上）期末数学试卷 题型：单选题

    a、b是有理数，如果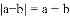，那么对于结论（1）a一定不是负数； （2）b可能是负数．其中（ ）

    A. 只有（1）正确

    B. 只有（2）正确

    C. （1），（2）都正确

    D. （1），（2）都不正确

    A 【解析】试题分析：根据绝对值的性质可得：a≥0，b≤0，则a一定不是负数，b一定不是正数．

    查看答案和解析>>

    科目：初中数学 来源：2017年四川省数学七年级（上）期末数学试卷 题型：单选题

    如图表示一个由相同小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，那么该几何体的主视图为（ ）

    C． 【解析】A、B、D不是该几何体的视图，C是主视图，故选C.

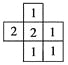
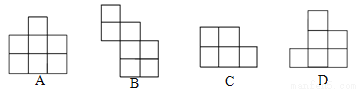
    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    计算：（1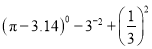） ；（2）.

    （1）1；（2） 【解析】试题分析：（1）原式第一项利用零指数幂法则计算，第二项利用负指数幂法则计算，最后一项表示两个的乘积，计算即可得到结果； （2）原式先利用积的乘方与幂的乘方运算法则计算，合并同类项即可得到结果． 试题解析：（1）原式= =1 （2）原式= =

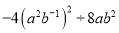    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    使分式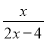有意义的条件是____________

    x≠2 【解析】试题解析：根据题意得：2x-4≠0， 解得：x≠2． 故答案为x≠2．

    查看答案和解析>>

    科目：初中数学 来源：贵州省2017-2018学年七年级（上）期中数学试卷 题型：填空题

    已知A=3x3+2x2﹣5x+7m+2，B=2x2+mx﹣3，若多项式A+B不含一次项，则多项式A+B的常数项是_____．

    34 【解析】∵A+B=（3x3+2x2﹣5x+7m+2）+（2x2+mx﹣3） =3x3+2x2﹣5x+7m+2+2x2+mx﹣3 =3x2+4x2+（m﹣5）x+7m﹣1 ∵多项式A+B不含一次项， ∴m﹣5=0，∴m=5， ∴多项式A+B的常数项是34， 故答案为：34

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省哈尔滨市双城区2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

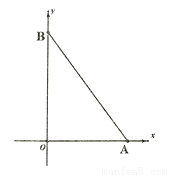
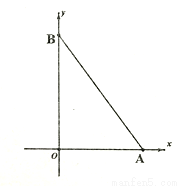
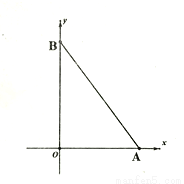
    如图，在平面直角坐标系中，点A坐标为(6，0)，点B在y轴的正半轴上，且=240.

    (1)求点B坐标；

    (2)若点P从B出发沿y轴负半轴方向运动，速度每秒2个单位，运动时间t秒，△AOP的面积为S，求S与t的关系式，并直接写出t的取值范围；

    (3)在(2)的条件下，若S△AOP：S△ABP=1:3，且S△AOP+S△ABP=S△AOB，在线段AB的垂直平分线上是否存在点Q，使得△AOQ的面积与△BPQ的面积相等？若存在，求出Q点坐标；若不存在，请说明理由。

    （1）点 B的坐标为（0,8）（2）S=24-6t (0≤t<4)； S=6t-24(t>4)；(3)点Q的坐标为(-1,1)或（7,7）. 【解析】试题分析：（1）根据三角形的面积公式求出OB的长即可； （2）分0≤t<4和t≥4两种情况，根据三角形面积公式计算即可； （3）根据题意和三角形的面积公式求出OP、BP的长，根据相似三角形的性质求出点E的坐标，根据中点的性质确定点F...

    查看答案和解析>>

    同步练习册答案