练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    我市5月的某一周每天的最高气温（单位：℃）统计如下：19，20，24，22，24，26，27，则这组数据的中位数与众数分别是（ ）

    A. 23，24 B. 24，22 C. 24，24 D. 22，24

    C 【解析】∵从小到大排列后排在中间位置的数是24，∴中位数是24； ∵出现次数最多的数是24，∴众数是24； 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省温州市2017-2018学年浙教版8年级上数学期末练习 题型：解答题

    如图，△ABC中，∠A=30°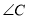，=90°，BE平分∠ABC，AC=9cm，求CE的长。

    CE=3cm 【解析】利用直角三角形的勾股定理和直角三角形30°所对的直角边等于斜边的一半

    查看答案和解析>>

    科目：初中数学 来源：新疆阿克苏十二中2017-2018学年八年级（上）期中数学试卷 题型：单选题

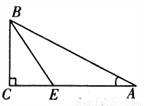
    如图：∠DAE=∠ADE=15°，DE∥AB，DF⊥AB，若AE=8，则DF等于（ ）

    A. 5 B. 4 C. 3 D. 2

    B 【解析】试题分析：过D作DG⊥AC于G，根据三角形的一个外角等于和它不相邻的两个内角的和求出∠DEG=30°，再根据直角三角形30°角所对的直角边等于斜边的一半求出DG=4，又DE∥AB，所以∠BAD=∠ADE，所以AD是∠BAC的平分线，根据角平分线上的点到角的两边的距离相等，得DF=DG=4． 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型：填空题

    已知抛物线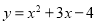与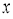轴的两个交点为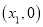、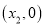则 ．

    28． 【解析】 试题分析：∵、为方程的两实根，∴，=-3；∴=（）+15=-3（）+19=9+19=28．故答案为28．

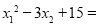    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型：单选题

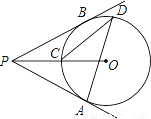
    如图，过⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，OP交⊙O于点C，点D是优弧 上不与点A、点C重合的一个动点，连接AD、CD，若∠APB=80°，则∠ADC的度数是（   ）

    A. 15° B. 20° C. 25° D. 30°

    C 【解析】试题分析：如图，由四边形的内角和定理，得 ∠BOA=360°﹣90°﹣90°﹣80°=100°，由=，得∠AOC=∠BOC=50°． 由圆周角定理，得∠ADC=∠AOC=25°，故选：C．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省鞍山市铁西区2017-2018学年七年级（上）期中数学试卷 题型：解答题

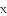
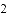
    已知，m、n互为相反数，p、q互为倒数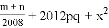，的绝对值为，求的值.

    2016 【解析】试题分析：由相反数和倒数的性质可求得m+n和pq，由绝对值的定义可求得x的值，代入计算即可． 【解析】 由题意可知m+n=0，pq=1，x=±2， ∴+2012pq+x2=+2012×1+（±2）2=0+2012+4=2016．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省鞍山市铁西区2017-2018学年七年级（上）期中数学试卷 题型：解答题

    把下列各数填在相应的表示集合的大括号内

    ﹣2，π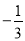， ，﹣|﹣3|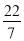， ，﹣0.3，1.7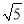， ，0，1.1010010001…

    整数{_____ …}

    负分数{_____…}

    无理数{_____…}．

    ﹣2，﹣|﹣3|，0 … ，﹣0.3 … π， ，1.1010010001… 【解析】试题分析：根据实数的分类方法即可判定求解．要注意的是π，1.1010010001…是无理数，开方开不尽的也是无理数．【解析】 整数{﹣2，﹣|﹣3|，0 …} 负分数{，﹣0.3 …} 无理数{ π， ，1.1010010001…}．

    查看答案和解析>>

    科目：初中数学 来源：福建省泉州台商投资区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型：解答题

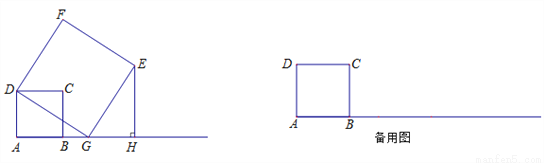
    在小学，我们知道正方形具有性质“四条边都相等，四个内角都是直角”，请适当利用上述知识，解答下列问题：

    已知：如图，在正方形ABCD中，AB=4，点G是射线AB上的一个动点，以DG为边向右作正方形DGEF，作EH⊥AB于点H．

    （1）填空：∠AGD+∠EGH=　 　°；

    （2）若点G在点B的右边．

    ①求证：△DAG≌△GHE；

    ②试探索：EH﹣BG的值是否为定值，若是，请求出定值；若不是，请说明理由．

    （3）连接EB，在G点的整个运动（点G与点A重合除外）过程中，求∠EBH的度数；

    （1）90；（2）①答案见解析；②EH﹣BG的值是定值4；（3）45°． 【解析】试题分析：（1）根据正方形的性质得到∠DGE=90°，由平角的定义即可得到结论； （2）①根据垂直的定义得到∠GHE=90°，根据余角的性质得到∠GEH=∠AGD，根据正方形的性质得到∠DAG=90°，DG=GE，求得∠DAG=∠GHE，根据全等三角形的判定定理即可得到结论；②根据全等三角形的性质得到AG=E...

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接AA′，若∠1=20°，则∠B的度数是（   ）

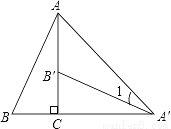
    A. 70° B. 65° C. 60° D. 55°

    B 【解析】试题分析：根据旋转图形可以得到△ACA′为等腰直角三角形，根据∠1的度数可以求出∠CA′B′=25°，从而得到∠CAB=25°，所以∠B=90°－25°=65°

    查看答案和解析>>

    同步练习册答案