
若式子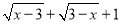 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A. x≥3 B. x≤3
C. x=3 D. 以上都不对
C 【解析】根据二次根式有意义的条件可得x-3≥0,3-x≥0,即可得x=3,故选C. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:黑龙江省安达市2017-2018学年七年级上学期期末质量检测数学试卷 题型:单选题
如图,小华的家在A处,书店在B处,星期日小明到书店去买书,他想尽快的赶到书店,请你帮助他选择一条最近的路线( ).

A. A→C→D→B B. A→C→F→B C. A→C→E→F→B D. A→C→M→B
C. A→C→E→F→B D. A→C→M→B
查看答案和解析>>
科目:初中数学 来源:山西大学附中2018届九年级10月月考数学试卷 题型:填空题
两对角线分别是 6cm 和 8cm 的菱形面积是_____cm2.
24 【解析】【解析】 ∵菱形的两条对角线分别是6cm和8cm,∴这个菱形的面积是: ×6×8=24(cm2).故答案为:24.查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:填空题
如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连结PE、PF、PG、PH,则△PEF和△PGH的面积和等于___________.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:单选题
如图,点O是矩形ABCD的对角线AC的中点,OM//AB交AD于点M,若OM=3,BC=10,则OB的长为( )

A. 5 B. 4 C.  D.
D. 
查看答案和解析>>
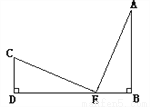
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
如图,CD⊥DB于D,AB⊥DB于B,CD=EB,AB=ED.
求证: (1)ΔCDE≌ΔEBA (2) CE⊥AE
证明:
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
计算:① 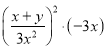 ②
②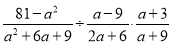
③ 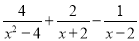 ④
④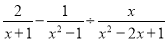
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
如图所示,在△ABC中,∠C=90°, AD是 ∠BAC的平分线,DE⊥AB交AB于E,F在AC上,BD=DF,证明:CF=EB.

查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:单选题
用一些不重叠的多边形把平面的一部分完全覆盖叫做平面镶嵌.则用一种多边形镶嵌时,下列多边形中不能进行平面镶嵌的是( )
A. 三角形 B. 正方形 C. 正五边形 D. 正六边形
C 【解析】几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角,360°为正多边形一个内角的整数倍才能单独镶嵌.由此可得三角形、正方形、正六边形用一种图形能够平面镶嵌,正五边形则不能,故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com