练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

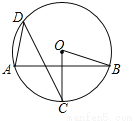
    如图，已知AB是⊙O的弦，半径OC垂直AB，点D是⊙O上一点，且点D与点C位于弦AB两侧，连接AD、CD、OB，若∠BOC=70°，则∠ADC=______度．

    35． 【解析】【解析】 如图，连接OA．∵OC⊥AB，∴ ，∴∠AOC=∠COB=70°，∴∠ADC=∠AOC=35°，故答案为：35．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型：单选题

    如图，DE∥BC,分别交△ABC的边AB、AC于点D、E, 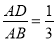, 若AE＝1，则EC=( )．

    A. 2 B. 3 C. 4 D. 6

    A 【解析】∵DE∥BC， ∴ ， ∵AE＝1， ∴AC=3 ∴EC=AC-AE=3-1=2． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（C卷） 题型：填空题

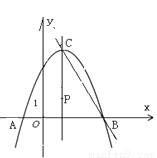
    如图，已知抛物线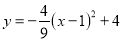，与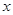轴交于A、B两点，点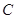为抛物线的顶点．点P在抛物线的对称轴上，设⊙P的半径为r，当⊙P与x轴和直线BC都相切时，则圆心P的坐标为___________ ．

    （1， ）或（1，-6） 【解析】设P点坐标为(1,a)， ∵抛物线的解析式为y=? (x?1)2+4， ∴抛物线顶点C的坐标为(1,4)， 令y=0,解得B点的坐标为(4,0)， 设直线BC的解析式为y=kx+b， ， 解得 ， 则直线BC的解析式为y=?x+， 点P到直线BC的距离 ， 点P到x轴的距离为|a|， 又知P与x轴和...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（C卷） 题型：单选题

    如图是一个标准的五角星，若将它绕旋转中心旋转一定角度后能与自身重合，则至少应将它旋转的度数是（ ）

    A. 144° B. 90° C. 72° D. 60°

    C 【解析】如图，设O的是五角星的中心， ∵五角星是正五角星， ∴∠AOB=∠BOC=∠COD=∠DOE=∠AOE， ∵它们都是旋转角，而它们的和为360°， ∴至少将它绕中心顺时针旋转360÷5=72°，才能使正五角星旋转后与自身重合． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（A卷） 题型：解答题

    已知二次函数y=﹣x2+bx+c的图象经过A（﹣2，﹣1），B（0，7）两点．

    （1）求该抛物线的解析式及对称轴；

    （2）当x为何值时，y＞0？

    （1）x=1；（2）当1﹣2＜x＜1+2时，y＞0 【解析】试题分析: （1）根据待定系数法求二次函数解析式，再用配方法或公式法求出对称轴即可； （2）求出二次函数与轴交点坐标即可，再利用函数图象得出取值范围； 试题解析：(1)∵二次函数的图象经过A(?2,?1),B(0,7)两点， 解得： ∴对称轴为：直线x=1. (2)当y=0， ∴抛物线与x轴交点坐标为...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（A卷） 题型：填空题

    如图，共有12个大小相同的小正方形，其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分，现从其余的小正方形中任取一个涂上阴影，能构成这个正方体的表面展开图的概率是_________.

    【解析】共有七种可能，其中能构成这个正方体的表面展开图的有： 共4种情况， 所以能构成这个正方体的表面展开图的概率是 ， 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（A卷） 题型：单选题

    已知△ABC和△DEF关于点O对称，相应的对称点如图所示，则下列结论正确的是（　　）

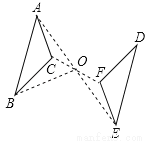
    A. AO=BO B. BO=EO

    C. 点A关于点O的对称点是点D D. 点D 在BO的延长线上

    D 【解析】根据中心对称的性质：中心对称点平分对应点连线的线段，可知： A.AO=OE，错误； B.BO=DO，错误； C.点A关于点O的对称点是点E，错误； D.点D在BO的延长线上，正确； 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级（上）第一次月考数学试卷 题型：填空题

    如图，△ABC≌△DEF，A与D，B与E分别是对应顶点，∠B=32°，∠A=68°，AB=13cm，则∠F=_____度，DE=_____cm．

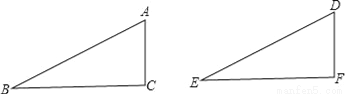
    80° 13cm 【解析】【解析】 ∵∠B=32°，∠A=68° ∴∠C=180°﹣32°﹣68°=80° 又△ABC≌△DEF ∴∠F=80°，DE=13cm．

    查看答案和解析>>

    科目：初中数学 来源：广西岑溪市2018届九年级上学期期中抽考数学试卷 题型：解答题

    某地要建造一个圆形喷水池，在水池中央垂直于水面安装一个花形柱子OA，O恰好在水面中心，安装在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，且在过OA的任一平面上，抛物线的形状如图（1）和（2）所示，建立直角坐标系，水流喷出的高度y（米）与水平距离x（米）之间的关系式是y=﹣x2+2x+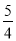，请回答下列问题．

    （1）柱子OA的高度为多少米？

    （2）喷出的水流距水平面的最大高度是多少？

    （3）若不计其他因素，水池的半径至少要多少米，才能使喷出的水流不至于落在池外？

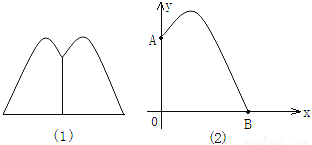
    （1）柱子OA的高度为米；（2）喷出的水流距水平面的最大高度是米；（3）水池的半径至少要3米，才能使喷出的水流不至于落在池外. 【解析】本题考查了二次函数的应用. （1）本题需先根据已知条件把x=0代入抛物线的解析式，从而得出y的值，即可求出答案． （2）通过抛物线的顶点坐标求得 （3）本题需先根据已知条件把y=0代入抛物线求出所要求的式子，再得出x的值，即可求出答案． ...

    查看答案和解析>>

    同步练习册答案