
已知一个多边形的内角和是这个多边形外角和的2倍,求这个多边形的边数?
6 【解析】试题分析:设这个多边形的边数为n,根据内角和公式和外角和公式,列出等式求解即可. 试题解析:设这个多边形的边数为n, 由题意得:(n?2)?180°=2×360°, 解得:n=6, 答:这个多边形的边数为6. 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源:山西大学附中2018届九年级10月月考数学试卷 题型:填空题
如图,在周长为 12 的菱形 ABCD 中,AE=1,AF=2,若 P 为对角线 BD 上一动点,则 EP+FP 的 最小值为 _____.
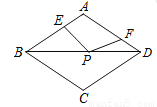
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
某化肥厂计划生产化肥120吨,由于采用了新技术,每天比计划多生产3吨,实际生产180吨与原计划生产120吨所用的时间相等,求计划每天生产几吨。
计划每天生产6吨 【解析】试题分析:设原计划每天生产x吨,则实际每天生产(x+3)吨,根据实际生产180吨与计划生产120吨所用的时间相同,列方程求解. 试题解析:设计划每天生产x吨, 由题意得, , 解得x=6, 经检验:x=6是原分式方程的解且符合题意. 答:计划每天生产6吨.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
因式分【解析】
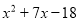 的结果为( )
的结果为( )
A. 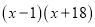 B.
B. 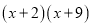 C.
C. 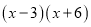 D.
D. 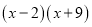
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
已知,如图,四边形ABCD中,E、F是对角线AC上两点,且 AE=CF,AB∥CD,AB=CD.求证:BE=DF

查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】根据全等三角形对应边相等,全等三角形对应角相等结合图象解答即可. ∵△ABC≌△AEF, ∴AC=AF,EF=BC,∠EAF=∠BAC,故(1)(3)正确, ∴∠EAF-∠BAF=∠BAC-∠BAF, 即∠EAB=∠FAC,故(4)正确, 只有AF平分∠BAC时,∠FAB=∠EAB正确,故(2)错误. 综上所述,正确的是(1)(3)(4)共3个. 故选C. ...查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:单选题
如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( )
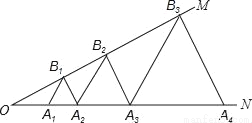
A. 6 B. 12 C. 32 D. 64
C 【解析】试题分析:;……,则,即△的边长为64.查看答案和解析>>
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
在平面直角坐标系中,将某点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这个点的“互换点”,如(-3,5)与(5,-3)是一对“互换点”.
(1)以O为圆心,半径为5的圆上有无数对“互换点”,请写出一对符合条件的“互换点”;
(2)点M,N是一对“互换点”,点M的坐标为(m,n),且(m>n),⊙P经过点M,N.
①点M的坐标为(4,0),求圆心P所在直线的表达式;
②⊙P的半径为5,求m-n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com