
��ƽ��ֱ������ϵ�У���ij�㣨�������������겻��ȣ��ĺ������������껥����õ��ĵ�������ġ������㡱���磨-3��5���루5��-3����һ�ԡ������㡱��
��1����OΪԲ�ģ��뾶Ϊ5��Բ���������ԡ������㡱����д��һ�Է��������ġ������㡱��
��2����M��N��һ�ԡ������㡱����M������Ϊ��m��n�����ң�m��n������P������M��N��
�ٵ�M������Ϊ��4��0������Բ��P����ֱ�ߵı���ʽ��
�ڡ�P�İ뾶Ϊ5����m��n��ȡֵ��Χ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��֪һ������ε��ڽǺ�������������Ǻ͵�2�������������εı�����
6 ��������������������������εı���Ϊn�������ڽǺ�ʽ����Ǻ�ʽ���г���ʽ��⼴�ɣ� ������������������εı���Ϊn�� ������ã�(n?2)?180��=2��360�㣬 ��ã�n=6�� ���������εı���Ϊ6.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2017-2018ѧ���һѧ�ڳ�����ѧ�����Ծ� ���ͣ������
��֪����ͼ��Rt��ABC�У���BAC=90��

��1����Ҫ����ͼ����������ͼ�ۼ���
���ӳ�BC����D��ʹCD=BC��
���ӳ�CA����E��ʹAE=2CA��
������AD��BE�������߶� AD��BE�Ĵ�С��ϵ��
��2��֤����1��������߶�AD��BE��С��ϵ�IJ��룮
������ �������������������1�����ݻ�����ͼ����һ���߶ε�����֪�߶ε���ͼ�����Ϳ�������ͼ�Σ� ��2���ӳ�AC����F��ʹCF=AF������BF��֤����ACD�ա�FCB������AD=FB�������ó�AE=AF���Ϳ��Եó�BE=BF���Ӷ�����AD=BE�� �����������1�������⣬����ͼ���£� ��2���ӳ�AC����F��ʹCF=AF������BF�� �ڡ�ACD�͡�FCB�У� CD=...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2017-2018ѧ���һѧ�ڳ�����ѧ�����Ծ� ���ͣ������
һ��ϸ���İ뾶Ϊ0.0004m ,�ÿ�ѧ��������ʾΪ____________m��
���������ɿ�ѧ����������֪��0.0004=�� �ʴ�Ϊ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2017-2018ѧ���һѧ�ڳ�����ѧ�����Ծ� ���ͣ���ѡ��
�ڡ�ABC�͡�A��B��C���У���֪��A=��A�䣬AB=A��B�䣬�������������е�һ��������ʹ��ABC �ա�A��B��C��һ���������ǣ� ����
A. AC=A��C�� B. BC=B��C�� C. ��B=��B�� D. ��C=��C��
B ���������������� A����A=��A�䣬AB=A��B��AC=A��C�䣬����SAS���Ƴ���ABC�ա�A��B��C�䣬��Aѡ����� B���߱���A=��A�䣬AB=A��B�䣬BC=B��C�䣬�����жϡ�ABC�ա�A��B��C�䣬��Bѡ����ȷ�� C������ASA���Ƴ���ABC�ա�A��B��C�䣬��Cѡ����� D������AAS���Ƴ���ABC�ա�A��B��C�䣬��Dѡ����� ��ѡB�� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ƽ����2018�������һѧ����ĩ��ѧ�Ծ� ���ͣ������
��ͼ���ڡ�ABCD�У��Խ���AC��BD���ڵ�O������O��EO��BD����BA�ӳ����ڵ�E����AD�ڵ�F����EF=OF����CBD=30�㣬BD=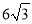 ����AF�ij���
����AF�ij���
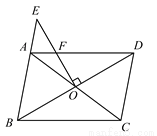
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ƽ����2018�������һѧ����ĩ��ѧ�Ծ� ���ͣ������
�����ǡ���һ���ǵ���30�㡱�ij߹���ͼ���̣�
��������ͼ����1��������AD��
��2��������AD������ȡһ��O����O�����A�غϣ���
��3���Ե�OΪԲ�ģ�OAΪ�뾶����O��������AD�ڵ�B��
��4���Ե�BΪԲ�ģ�OBΪ�뾶����������O�ڵ�C��
��5��������AC��
��DAC��Ϊ��������30��ǣ�
��ش𣺸ó߹���ͼ��������_________________��
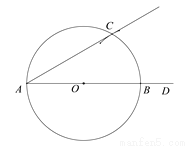
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
ijũ����������һ��ũ����Ʒ����֪���ֲ�Ʒ�ijɱ���Ϊ20Ԫ/ǧ�ˣ��г����鷢�֣��ò�Ʒÿ���������w ��ǧ�ˣ������ۼ�x ��Ԫ/ǧ�ˣ������¹�ϵ��w=��2x+80�������ֲ�Ʒÿ�����������Ϊy ��Ԫ����
��1����y��x֮��ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��2�������ۼ۶�Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
��3�������۲��Ź涨���ֲ�Ʒ�����ۼ۲��ø���28Ԫ/ǧ�ˣ���ũ����Ҫÿ����150Ԫ�������������ۼ�Ӧ��Ϊ����Ԫ�����ο���ϵ�����۶�=�ۼۡ�����������=���۶�ɱ���
(1) y=��2x2+120x��1600��20��x��40��(2) 30Ԫ/ǧ��, 200Ԫ����3��25. �������� �����������1��������������y=��ÿǧ�����ۼ۩�ÿǧ�˳ɱ��ۣ���������w�������г�y��x֮��ĺ�����ϵʽ�� ��2���������䷽������1���ĺ�����ϵʽ���Σ������ö��κ��������ʼ�����⣻ ��3���Ȱ�y=150���루1���ĺ�����ϵʽ�У���һԪ���η������x���ٸ���x...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ϻ��ֶ�����2017-2018ѧ����꼶��ѧ����ĩ��ѧ�Ծ�������һģ�� ���ͣ���ѡ��
��ͼ����֪��D��F�ڡ�ABC�ı�AB�ϣ���E�ڱ�AC�ϣ���DE��BC��Ҫʹ��EF��CD����������һ���������������������
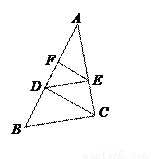
A. 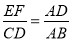 �� B.
�� B. 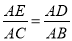 ��
��
C. 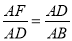 �� D.
�� D. 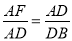 ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com