
下列所给图形既是中心对称图形,又是轴对称图形的是
A. 正三角形 B. 角 C. 正方形 D. 正五边形
C 【解析】选项A. 正三角形是轴对称图形. 选项B. 角是轴对称图形. 选项 C. 正方形既是中心对称图形,又是轴对称图形. 选项D. 正五边形是轴对称图形. 故选C.科目:初中数学 来源:江西婺源县2016-2017学年第一学期期末考试九年级数学试卷 题型:解答题
某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
(1)y=﹣5x2+800x﹣27500(50≤x≤100);(2)当销售单价为80元时,y最大值=4500;(3)销售单价应该控制在82元至90元之间. 【解析】试题分析: (1)由“商品利润”=“商品售价”-“商品成本价”和“总利润”=“单件商品利润” “商品销售量”结合题意可列出函数关系式; (2)把(1)中所得函数解析式配方,再由题意求得自变量的取值范围,就可在自变量的取...查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型:填空题
已知扇形的面积为6π,半径为4,则该扇形的弧长为_______ .
3π 【解析】 , ∴ .查看答案和解析>>
科目:初中数学 来源:河南省2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在△ABC中,∠C=90°,AC=BC=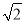 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B= ______
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B= ______
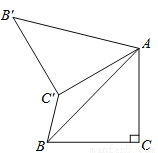
查看答案和解析>>
科目:初中数学 来源:河南省2018届九年级上学期期末考试数学试卷 题型:单选题
如图,PA、PB是⊙O的两条切线,切点分别是A、B,如果OP=4,PA=2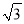 ,那么
,那么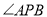 等于
等于
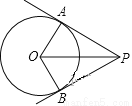
A. 90° B. 100° C. 60° D. 110°
C 【解析】cos∠APO==,所以∠APO=30°, .所以选C.查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市翁牛特旗2018届九年级上学期期末考试数学试卷 题型:解答题
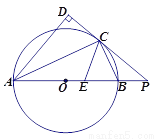
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
(1)求证:AC平分∠DAB;
(2)求证:△PCE是等腰三角形.
查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市翁牛特旗2018届九年级上学期期末考试数学试卷 题型:填空题
如图,一个半径为2cm的圆盘被分割成十个区域. 其中,弦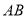 、
、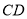 关于圆心
关于圆心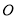 对称,
对称, 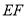 、
、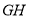 关于圆心
关于圆心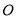 对称,向盘中投掷一物体,则物体落在阴影部分的概率为_____________.
对称,向盘中投掷一物体,则物体落在阴影部分的概率为_____________.
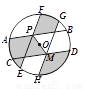
查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:解答题
“不览夜景,味道重庆.”乘游船也有两江,犹如在星河中畅游,是一个近距离认识重庆的最佳窗口.“两江号”游轮经过核算,每位游客的接待成本为30元.根据市场调查,同一时段里,票价为40元时,每晚将售出船票600张,而票价每涨1元,就会少售出10张船票.
(1)若该游轮每晚获得10000元利润的同时,适当控制游客人数,保持应有的服务水准,则票价应定为多少元?
(2)春节期间,工商管理部门规定游轮船票单价不能低于44元,同时该游轮为提高市场占有率,决定每晚售出船票数量不少于540张,则票价应定为多少元,才能使每晚获得的利润最多?
(1)80元(2)票价应定为46元时,最大利润为8640元. 【解析】 试题分析:(1)设票价应定为x元,然后根据每晚获得10000元利润列一元二次方程,然后解方程即可;(2)设每晚获得的利润为W元,然后求出w与x的二次函数关系式,利用配方法化为顶点式,结合抛物线的性质和自变量的取值范围解决问题即可. 试题解析:(1)设票价应定为x元,由题意,得 (x-30)[600-10...查看答案和解析>>
科目:初中数学 来源:湖北省元月联合测试数学试卷 题型:单选题
下列事件属于随机事件的是( )
A. 任意画一个三角形,其内角和为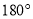 B. 经过有交通信号灯的路口,遇到红灯
B. 经过有交通信号灯的路口,遇到红灯
C. 掷一次骰子,向上一面点数是7 D. 明天的太阳从东方升起
B 【解析】选项A、D是必然事件;选项C是不可能事件;选项B是随机事件.故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com