
������ҹ����ζ�����죮�����δ�Ҳ���������������Ǻ��г��Σ���һ����������ʶ�������Ѵ��ڣ��������š����־������㣬ÿλ�ο͵ĽӴ��ɱ�Ϊ30Ԫ�������г����飬ͬһʱ���Ʊ��Ϊ40Ԫʱ��ÿ�����۳���Ʊ600�ţ���Ʊ��ÿ��1Ԫ���ͻ����۳�10�Ŵ�Ʊ��
��1����������ÿ�����10000Ԫ�����ͬʱ���ʵ������ο�����������Ӧ�еķ���ˮ����Ʊ��Ӧ��Ϊ����Ԫ��
��2�������ڼ䣬���̹������Ź涨���ִ�Ʊ���۲��ܵ���44Ԫ��ͬʱ������Ϊ����г�ռ���ʣ�����ÿ���۳���Ʊ����������540�ţ���Ʊ��Ӧ��Ϊ����Ԫ������ʹÿ����õ�������ࣿ
��1��80Ԫ��2��Ʊ��Ӧ��Ϊ46Ԫʱ���������Ϊ8640Ԫ�� �������� �����������1����Ʊ��Ӧ��ΪxԪ��Ȼ�����ÿ�����10000Ԫ������һԪ���η��̣�Ȼ��ⷽ�̼��ɣ���2����ÿ����õ�����ΪWԪ��Ȼ�����w��x�Ķ��κ�����ϵʽ�������䷽����Ϊ����ʽ����������ߵ����ʺ��Ա�����ȡֵ��Χ������⼴��. �����������1����Ʊ��Ӧ��ΪxԪ�������⣬�� ��x-30��[600-10...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ���Ƹ��й�����2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
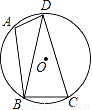
��ͼ����֪�ı���ABCD�ڽ���ԲO����A=105�㣬BD=CD��
��1�����DBC�Ķ�����
��2������O�İ뾶Ϊ3���� �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��������ͼ�μ������ĶԳ�ͼ�Σ�������Գ�ͼ�ε���
A. �������� B. �� C. ������ D. �������
C ��������ѡ��A. ������������Գ�ͼ��. ѡ��B. ������Գ�ͼ��. ѡ�� C. �����μ������ĶԳ�ͼ�Σ�������Գ�ͼ��. ѡ��D. �����������Գ�ͼ��. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹų������ţ����2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ���ı���PAOB������OMN���ڽӾ��Σ�����P��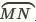 �ϣ��Ҳ���M��N�غϣ���P����
�ϣ��Ҳ���M��N�غϣ���P����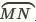 ���ƶ�ʱ������PAOB����״����С��֮�仯����AB�ij���( )
���ƶ�ʱ������PAOB����״����С��֮�仯����AB�ij���( )
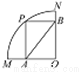
A. ��� B. ��С C. ���� D. ����ȷ��
C �����������������PAOB������OMN���ڽӾ��Σ����ݾ��ε�����AB=OP=�뾶������AB���Ȳ��䣮 ��ѡ��C�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹų������ţ����2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��֪���������ɸ�������ֻ��2���������dz���ɫ����������ͬ���������������һ������������ĸ�����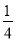 �����������ܸ����ǣ�������
�����������ܸ����ǣ�������
A. 2 B. 4 C. 6 D. 8
D �������������������������ܸ����ǣ�2��=8�������� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����������ɽ��2018����꼶��ѧ�ڰ�У������ѧ�Ծ� ���ͣ������
��ͼ��һ�������ߣ�y= -x��x-3����0��x��3������ΪC1������x�ύ�ڵ�O��A1��
��C1�Ƶ�A1��ת180���C2����x���ڵ�A2��
��C2�Ƶ�A2��ת180���C3����x���ڵ�A3��
����
��˽�����ȥ��ֱ����C10����P��28��m���ڵ�14��������C10�ϣ���m= ______ ��
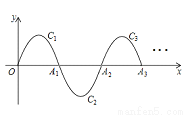
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����������ɽ��2018����꼶��ѧ�ڰ�У������ѧ�Ծ� ���ͣ���ѡ��
��ͼ��ʾ��һ����Ӱ뾶Ϊ2�ġ�O�ϵ�A0���������������A0O�����˶�����O�ϵĵ�A1��������������������A1O�н�Ϊ60��ķ����˶�����O�ϵĵ�A2���������ִ�A2���������������A2O�����˶�����O�ϵĵ�A3��������������������A3O�н�Ϊ60��ķ����˶�����O�ϵĵ�A4���������˹����˶�����A2018�������A2018���A0��ľ����ǣ�������
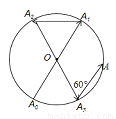
A. 0 B. 2 C. 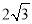 D. 4
D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡԪ�����ϲ�����ѧ�Ծ� ���ͣ������
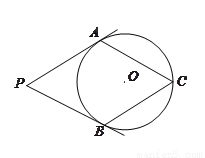
��ͼ�� 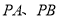 �ֱ���
�ֱ���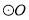 ������
������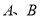 ���㣬��
���㣬��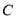 ��
��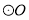 �ϣ���P=60º��
�ϣ���P=60º��
��1����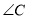 �Ķ�����
�Ķ�����
��2����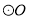 �뾶Ϊ1����
�뾶Ϊ1����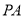 �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹź��ͺ����о��꼶���£�������ѧ�Ծ� ���ͣ������
��֪���κ���y=x2����2k+1��x+k2+k��k��0��
��1����k=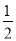 ʱ����������κ����Ľ���ʽд�ɶ���ʽ��
ʱ����������κ����Ľ���ʽд�ɶ���ʽ��
��2����֤������x��һԪ���η���x2����2k+1��x+k2+k=0����������ȵ�ʵ������
��1����1�� ����2��֤�������� �������������������1����k���������߽���ʽ��Ȼ�������䷽����ȷ�������ߵĶ������ꣻ��2�������б�ʽ��ֵ��Ȼ���б�ʽ���������֤���� �����������1����k=����y=x2����2k+1��x+k2+k��k��0����y=x2��2x+�� ��Ϊy=��x��1��2�� ���������ߵĶ�������Ϊ��1���� ���� ��2����=��2k+1��2��4��k2+k��=1��0...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com