如图，点A，B，C在⊙O上，若∠BAC＝45°，OB＝2，则图中阴影部分的面积为( )
A. π－4 B. 
π－1 C. π－2 D. 
－2
【答案】C
【解析】试题解析：∵∠BAC=45°，
∴∠BOC=90°，
∴△OBC是等腰直角三角形，
∵OB=2，
∴△OBC的BC边上的高为：
OB=
，
∴BC=2
∴S阴影=S扇形OBC﹣S△OBC=
.
故选C．
【题型】单选题
【结束】
9
已知二次函数的图象如图，则下列结论中正确的有（ ）
①a＋b＋c＞0；②a－b＋c＜0；③b＞0；④b＝2a；⑤abc＜0.
A. 5个 B. 4个 C. 3个 D. 2个
阅读快车系列答案科目：初中数学 来源：北京市2018届初三数学中考复习 综合练习题 含答案 题型：填空题
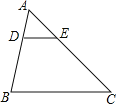
如图，△ABC中，D、E分别在AB、AC上，DE∥BC，AD：AB=1：3，则△ADE与△ABC的面积之比为______．
查看答案和解析>>
科目：初中数学 来源：天津市2018届初三数学中考复习综合检测题 题型：解答题
已知：如图，在△ABC中，AB=AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E．
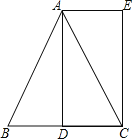
（1）求证：△ABD≌△CAE；
（2）连接DE，线段DE与AB之间有怎样的位置和数量关系？请证明你的结论．
【答案】（1）证明详见解析；（2）AB∥DE，AB=DE，理由详见解析．
【解析】试题分析：（1）运用AAS证明△ABD≌△CAE；
（2）易证四边形ADCE是矩形，所以AC=DE=AB，也可证四边形ABDE是平行四边形得到AB=DE．
试题解析：证明：（1）∵AB=AC，
∴∠B=∠ACD，
∵AE∥BC，
∴∠EAC=∠ACD，
∴∠B=∠EAC，
∵AD是BC边上的中线，
∴AD⊥BC，
∵CE⊥AE，
∴∠ADC=∠CEA=90°
在△ABD和△CAE中
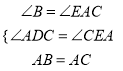
∴△ABD≌△CAE（AAS）；
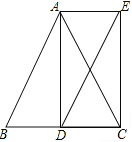
（2）AB∥DE，AB=DE，理由如下：
如图所示，
∵AD⊥BC，AE∥BC，
∴AD⊥AE，
又∵CE⊥AE，
∴四边形ADCE是矩形，
∴AC=DE，
∵AB=AC，
∴AB=DE，
∵AE∥BC，
∴四边形ABDE是平行四边形，
∴AB∥DE，AB=DE．
考点：全等三角形的判定与性质；等腰三角形的性质；平行四边形的判定与性质．
【题型】解答题
【结束】
21
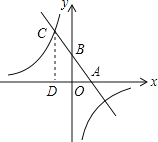
已知，如图，一次函数y=kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=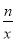
（n为常数且n≠0）的图象在第二象限交于点C．CD⊥x轴，垂直为D，若OB=2OA=3OD=6．
（1）求一次函数与反比例函数的解析式；
（2）求两函数图象的另一个交点坐标；
（3）直接写出不等式；kx+b≤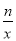
的解集．
查看答案和解析>>
科目：初中数学 来源：天津市2018届初三数学中考复习综合检测题 题型：填空题
函数
中自变量
【答案】x<1
【解析】试题解析：
由题意得，1-x>0，
解得x<1．
【点睛】本题考查了函数自变量的范围，一般从三个方面考虑：
（1）当函数表达式是整式时，自变量可取全体实数；
（2）当函数表达式是分式时，考虑分式的分母不能为0；
（3）当函数表达式是二次根式时，被开方数非负．
【题型】填空题
【结束】
14
如图，把平行四边形ABCD折叠，使点C与点A重合，这时点D落在D1，折痕为EF，若∠BAE=55°，则∠D1AD=__．
查看答案和解析>>
科目：初中数学 来源：天津市2018届初三数学中考复习综合检测题 题型：单选题
下列运算正确的是( )
A. a2＋4a－4＝(a＋2)2 B. a2＋a2＝a4
C. (－2ab)2＝－4a2b2 D. a4÷a＝a3
查看答案和解析>>
科目：初中数学 来源：四川省2018届九年级下学期二诊考试数学试卷 题型：填空题
如图，在矩形ABCD中，AB=2，BC=4，⊙D的半径为1．现将一个直角三角板的直角顶点与矩形的对称中心O重合，绕着O点转动三角板，使它的一条直角边与⊙D切于点H，此时两直角边与AD交于E，F两点，则tan∠EFO的值为_____．
查看答案和解析>>
科目：初中数学 来源：四川省2018届九年级下学期二诊考试数学试卷 题型：单选题
下列命题中,假命题有( )
①两点之间线段最短;
②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;
④垂直于同一直线的两条直线平行;
⑤若
的弦AB,CD交于点P,则
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
B. 
C. 
D. 