
��ͼ,�����������е�ÿ��С�����α߳�����1,ÿ��С��Ķ���������,�Ը��Ϊ����ֱ�����Ҫ��������.
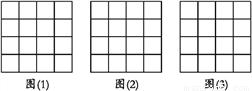
(1)��ͼ(1)��,��һ��������,ʹ�������߳�����������;
(2)��ͼ(2)��,��һ��ֱ��������,ʹ���ǵ����߳�����������;
(3)��ͼ(3)��,��һ��������,ʹ���������10.
�������. �������������������1����һ���߳�3��4��5�������μ��ɣ���2�����ù��ɶ������ҳ�Ϊ���������߶Σ��������μ��ɣ���3�����߳�Ϊ�������μ��ɣ� ��������� (1)���߷ֱ�Ϊ3,4,5(��ͼ(1)); (2)���߷ֱ�Ϊ (��ͼ(2)); (3)��һ���߳�Ϊ��������(��ͼ(3)). �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ڶ�ѧ�������л�ɽ����һ��ѧ��ĩ�Ծ� ���ͣ���ѡ��
���������У���ȷ���ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017ѧ��ζ�����һѧ�ھ��꼶����ѧҵ�������в��ԣ�2018�����һģ�� ���ͣ������
�������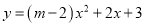 ��
��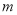 Ϊ�������Ƕ��κ�������ô
Ϊ�������Ƕ��κ�������ô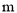 ȡֵ��Χ�� ____��
ȡֵ��Χ�� ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ����ѧ����2018����꼶10���¿���ѧ�Ծ� ���ͣ������
ij��ҩƷ�������ν�����ԭ����ÿ�� 12.5 Ԫ����ÿ�� 8 Ԫ����� 2 �ν��۵İٷ�����ͬ����ÿ�ν��۵İٷ���Ϊ x�����г��ķ���Ϊ_____.
12.5(1-x)2=8 ���������������� ��������ã�12.5��1��x��2=8���ʴ�Ϊ��12.5��1��x��2=8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ����ѧ����2018����꼶10���¿���ѧ�Ծ� ���ͣ���ѡ��
��ͼ��������ABCD�У�AC��8��BD��6�����ABD���ܳ�����(����)

A. 18 B. 16 C. 15 D. 14
B ����������֪�ı���ABCD�����Σ�AC=8, BD=6���������ε����ʿɵ�OA=4,OD=3,AB=AD,��Rt��AOD�У��ɹ��ɶ����ɵ�AD=5�����ԡ�ABD���ܳ�����AD+AB+BD=5+5+6=16,��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���˽̰���꼶��ѧ�²���в��� ���ͣ������
��֪a,bΪһ�����������ε������߳�,������b=2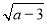 +
+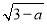 +5,��˵��������ε��ܳ�.
+5,��˵��������ε��ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���˽̰���꼶��ѧ�²���в��� ���ͣ���ѡ��
��֤:���ε������Խ����ഹֱ.
��֪:��ͼ,�ı���ABCD������,�Խ���AC,BD���ڵ�O.��֤:AC��BD.

���������ҵ�֤������:
����BO=DO;
�ڡ�AO��BD,��AC��BD;
�ۡ��ı���ABCD������;
�ܡ�AB=AD.
֤��������ȷ��˳����( ��)
A. �ۡ��ڡ��١��� B. �ۡ��ܡ��١���
C. �١��ڡ��ܡ��� D. �١��ܡ��ۡ���
B ������������������������ȵ����ʿɵ�AB=AD��OB=OD�����ݵ������������ߺ�һ�����ʿɵ�AO��BD�����ɵ�AC��BD��������ȷ��˳��Ϊ�ۡ��ܡ��١��ڣ���ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2017-2018ѧ���һѧ�ڳ�����ѧ�����Ծ� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ���س���2016���^���꼶��ĩ�����Ծ� ���ͣ������
��1����ͼ����A=��D=90�㣬BEƽ�֡�ABC���ҵ�E��AD���е㣬��֤��BC=AB+CD��

��2����ͼ����ACB�͡�ECD���ǵȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
����֤��AD=BE��
�����AEB�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com