
(1)如图,∠A=∠D=90°,BE平分∠ABC,且点E是AD的中点,求证:BC=AB+CD.

(2)如图,△ACB和△ECD都是等边三角形,点A、D、E在同一直线上,连接BE.
①求证:AD=BE;
②求∠AEB的度数.

科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:解答题
如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
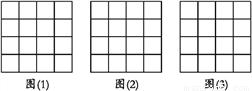
(1)在图(1)中,画一个三角形,使它的三边长都是有理数;
(2)在图(2)中,画一个直角三角形,使它们的三边长都是无理数;
(3)在图(3)中,画一个正方形,使它的面积是10.
详见解析. 【解析】试题分析:(1)画一个边长3,4,5的三角形即可;(2)利用勾股定理,找长为无理数的线段,画三角形即可;(3)画边长为的正方形即可. 试题解析: (1)三边分别为3,4,5(如图(1)); (2)三边分别为 (如图(2)); (3)画一个边长为的正方形(如图(3)).查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
若分式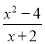 的值为0,则x应满足的条件是( )
的值为0,则x应满足的条件是( )
A. 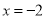 B.
B. 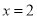 C.
C. 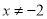 D.
D. 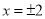
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
已知直角坐标系中,A(2a-5,7)、B(3,b)关于x轴对称,则式子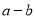 的值是__________.
的值是__________.
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
如图,AB∥DE,CD=BF,若要证明△ABC≌△EDF,还需补充的条件是( )
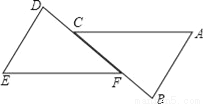
A. AC=EF B. AB=ED C. ∠B=∠E D. 不用补充
B 【解析】试题分析:根据平行线的性质得出∠B=∠D,求出BC=DF,根据全等三角形的判定定理逐个判断即可. 【解析】 AB=DE, 理由是:∵AB∥DE, ∴∠B=∠D, ∵BF=DC, ∴BC=DF, 在△ABC和△DEF中 , ∴△ABC≌△DEF(SAS),即选项B正确, 选项A、C、D都不能推出△ABC≌△DEF,即选项A、C...查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:填空题
已知x2+y2=25,xy=12,,则x+y的值为___________
±7. 【解析】∵x2+y2=25,xy=12, ∴(x+y)2=x2+2xy+y2=25+2×12=49, ∴x+y=±7.查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:单选题
已知关于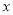 的分式方程
的分式方程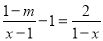 的解是正数,则
的解是正数,则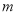 的取值范围是( )
的取值范围是( )
A. 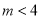 且
且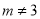 B.
B. 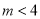
C. 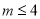 且
且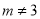 D.
D. 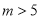 且
且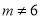
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
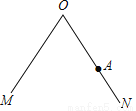
如图,∠MON及ON上一点A.
求作:点P,使得PA⊥ON,且点P到∠MON两边的距离相等.
查看答案和解析>>
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:填空题
已知菱形ABCD中,∠B=60°,AB=2,则菱形ABCD的面积是_________________.
【解析】如图,作AE⊥BC于点E. ∵四边形ABCD是菱形,,AB=2, ∴BC=AB=2. ∵ , ∴AE=sin60°×2= , ∴菱形ABCD的面=BC·AE= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com