练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    求证:等腰三角形的两底角相等.

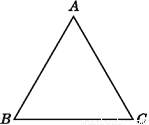
    已知:如图,在△ABC中,AB=AC.

    试说明:∠B=∠C.

    答案见解析 【解析】试题分析：过点A作AD⊥BC于点D，由三线合一性质得到BD=DC，从而求得△ABD≌△ACD，根据全等三角形的性质就可以得出∠B=∠C． 试题解析：过点A作AD⊥BC于点D，∵AB=AC，AD⊥BC，∴BD=DC（等腰三角形三线合一）．又∵∠ADB=∠ADC=90°，AD为公共边，在△ABD与△ACD中，∵BD=DC，∠ADB=∠ADC，AD=AD，∴△ABD≌△A...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型：单选题

    已知在同一平面内:①两条直线相交成直角;②两条直线互相垂直;③一条直线是另一条直线的垂线.那么下列因果关系:①→②③;②→①③;③→①②中,正确的有(　　)

    A. 0个 B. 1个 C. 2个 D. 3个

    D 【解析】垂直的定义：再同一平面内，两条直线相交成直角时，称这两条直线互相垂直，其中一条直线是另一条直线的垂线.由此可知三种因果关系都正确. 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：填空题

    (1)若2m=3,2n=5，则4m＋n=____；

    (2)若3x=4,9y=7，则3x－2y的值为____.

    225 【解析】（1）∵4m=(2m)2=9,4n=(2n)2=25， ∴4m+n=4m×4n=9×25=225， （2）3x－2y=3x÷32y=3x÷9y=4÷7= . 故答案为：225，

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下3.2 用关系式表示的变量间关系 同步练习 题型：单选题

    一个长方体的体积为12 cm3,当底面积不变,高增大时,长方体的体积发生变化,若底面积不变,高变为原来的3倍,则体积变为(　　)

    A. 12 cm3 B. 24 cm3 C. 36 cm3 D. 48 cm3

    C 【解析】设长方体的底面积为s，高为h，则其体积v=sh， ∴当长方体的底面积不变，高变为原来的3倍时，其体积也变为原来的3倍， ∴若原来的体积为12cm3，则现在的体积为：36cm3.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下3.2 用关系式表示的变量间关系 同步练习 题型：单选题

    有一本书,每20页厚1 mm,设从第1页到第x页的厚度为y mm,则(　　)

    A. y=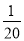x B. y=20x C. y=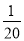+x D. y=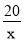

    A 【解析】∵这本书每20页厚1mm， ∴这本书每页厚为mm， ∴. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型：解答题

    如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD=BE,△ADC与△AEB全等吗?请说明理由.

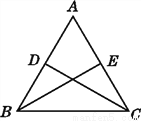
    答案见解析 【解析】试题分析：由中点定义及AB=AC，可得到AD=AE，再通过SAS证明△ADC≌△AEB即可． 试题解析：【解析】 △ADC≌△AEB．理由如下： ∵AB=AC，D，E分别是AB，AC的中点，∴AD=AE． 在△ADC和△AEB中，∵AC=AB，∠A=∠A(公共角)，AD=AE， ∴△ADC≌△AEB(SAS)．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型：单选题

    如图，点E，F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加的一个条件是（　　）

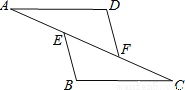
    A. ∠A=∠C B. ∠D=∠B C. AD∥BC D. DF∥BE

    B 【解析】试题分析：利用全等三角形的判定与性质进而得出当∠D=∠B时，△ADF≌△CBE． 当∠D=∠B时， 在△ADF和△CBE中 ∵， ∴△ADF≌△CBE（SAS）

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第四章4.4用尺规作三角形课时练习 题型：解答题

    已知：线段a，∠α．

    求作：△ABC，使AB=BC=a，∠B=∠α．

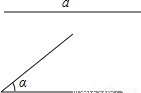
    见解析 【解析】 试题分析：可做∠A=∠α，然后在∠A的两边上分别截取AC=AB=a，连接BC即可． 试题解析：【解析】

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.1 用“边边边”判定三角形全等 同步练习 题型：解答题

    如图：AB=AC，AD=AE，BE=CD，试说明：△ABD≌△ACE.

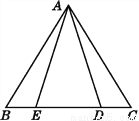
    证明见解析. 【解析】试题分析：根据等腰三角形的性质得出∠ADB=∠AEC，∠B=∠C，进而利用全等三角形的判定方法即可得出全等三角形． 试题解析： 证明：∵AD=AE， ∴∠ADE=∠AED， ∴∠ADB=∠AEC， ∵AB=AC， ∴∠B=∠C， 在△ABD和△ACE中 ∠B=∠C，∠BDA=∠CEA，AD=AE， ∴△ABD≌△AC...

    查看答案和解析>>

    同步练习册答案