
已知在同一平面内:①两条直线相交成直角;②两条直线互相垂直;③一条直线是另一条直线的垂线.那么下列因果关系:①→②③;②→①③;③→①②中,正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
D 【解析】垂直的定义:再同一平面内,两条直线相交成直角时,称这两条直线互相垂直,其中一条直线是另一条直线的垂线.由此可知三种因果关系都正确. 故选:D. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:北师大版七年级数学下册达标检测 第三章 变量之间的关系 题型:填空题
如图是甲、乙两名运动员在自行车比赛中所走路程与时间的关系图象,则甲的速度____________乙的速度(用“>”“=”或“<”填空).
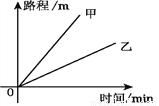
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册4.2图形的全等练习 题型:单选题
已知图中的两个三角形全等,则∠α的度数是( )
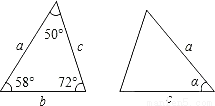
A. 72° B. 60° C. 58° D. 50°
D 【解析】 由图像可得:△ABC≌△DEF, ∴∠A=∠D=50°,∠C=∠F=72°, ∴∠1=180°-50°-72°=58°. 故选C.查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第五章达标检测卷 题型:单选题
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
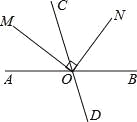
A. 35° B. 45° C. 55° D. 65°
C 【解析】因为ON⊥OM,∠CON=55°,所以∠COM=90°-∠CON=90°-55°=35°, 又因为OM平分∠AOC,所以∠AOC=∠COM=35°,故选A.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:单选题
如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
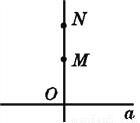
A. 过两点只有一条直线
B. 在同一平面内,过两点有且只有一条直线与已知直线垂直
C. 在同一平面内,过一点有且只有一条直线与已知直线垂直
D. 两点之间,线段最短
C 【解析】因为OM⊥直线a,ON⊥直线a,所以直线ON与OM重合, 其理由是:过一点有且只有一条直线垂直于已知直线. 故选:C.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册4.1.2认识三角形 同步练习 题型:解答题
一个不等边三角形的边长都是整数,且周长是12,这样的三角形共有多少个?
符合条件的三角形共有1个 【解析】试题分析:题设中已知数较少,只知道周长为12,应抓住不等边三角形的边长都是整数这一条件,依据三角形三边关系先确定出最大边的取值范围,则问题迎刃而解. 试题解析:设 a<b<c,则a+b+c>2c,即 2c<12,所以 c<6, 因为a,b,c 都是正整数,所以若c=3,则其他两边必然为a=1,b=2, 由于1+2=3,即 a+b=c,故线段...查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册4.1.2认识三角形 同步练习 题型:单选题
如图,用四个螺丝将四条不可弯曲的木条围成一个木框(形状不限),不计螺丝大小,其中相邻两螺丝的距离依次为3、4、5、7,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( )
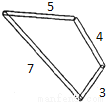
A. 6 B. 7 C. 8 D. 9
D 【解析】已知4条木棍的四边长为2、3、4、6; ①选3+4、5、7作为三角形,则三边长为7、5、7,能构成三角形,此时两个螺丝间的最长距离为7; ②选4+5、7、3作为三角形,则三边长为9、7、3,能构成三角形,此时两个螺丝间的最大距离为9; ③选5+7、3、4作为三角形,则三边长为12、3、4,不能构成三角形,此种情况不成立; ④选7+3、4、5作为三角形,则三...查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册同步要点3.2 用关系式表示的变量间关系 题型:单选题
一长为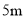 ,宽为
,宽为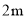 的长方形木板,现要在长边上截去长为
的长方形木板,现要在长边上截去长为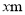 的一部分(如图),则剩余木板的面积
的一部分(如图),则剩余木板的面积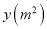 与
与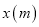 的关系式为(其中
的关系式为(其中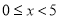 )( ).
)( ).

A. 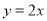 B.
B. 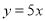 C.
C. 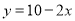 D.
D. 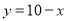
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型:解答题
求证:等腰三角形的两底角相等.
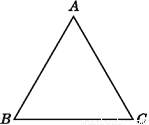
已知:如图,在△ABC中,AB=AC.
试说明:∠B=∠C.
答案见解析 【解析】试题分析:过点A作AD⊥BC于点D,由三线合一性质得到BD=DC,从而求得△ABD≌△ACD,根据全等三角形的性质就可以得出∠B=∠C. 试题解析:过点A作AD⊥BC于点D,∵AB=AC,AD⊥BC,∴BD=DC(等腰三角形三线合一).又∵∠ADB=∠ADC=90°,AD为公共边,在△ABD与△ACD中,∵BD=DC,∠ADB=∠ADC,AD=AD,∴△ABD≌△A...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com