
��ȫ�����������̣�
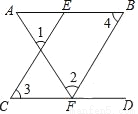
��ͼ����֪��1=��2����3=��4����˵��AB��CD��
��������
�ߡ�1=��2����֪��
��CE��FB ���� ����
���4=��AEC ���� ����
�ߡ�3=��4 �� ��֪��
���3=��AEC ���� ����
��AB��CD���� ����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ������꼶��ѧ�ϲ���ĩ���Ծ� ���ͣ������
��3�ĵ�����________��
�����������ݵ����Ķ��壺���������ij˻���1�����Ǿͳ�����������Ϊ������ ��𣺡������� -3�ĵ�����-���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
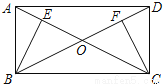
��֪:��ͼ��ƽ���ı���ABCD�������Խ����ཻ�ڵ�O��BE��AC��CF��BD������ֱ�ΪE��F����BE=CF��
��֤��ƽ���ı���ABCD�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У�AB=3��AC=4��BC=5��PΪ��BC��һ���㣬PE��AB��E��PF��AC��F����EF����СֵΪ�� ��
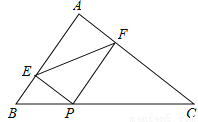
A. 2 B. 2.2 C. 2.4 D. 2.5
C �����������������Ƕ���ֱ�ǵ��ı����Ǿ��Σ����ı���AEPF�Ǿ��Σ����ݾ��εĶԽ�����ȣ���EF=AP����EF����Сֵ��ΪAP����Сֵ�����ݴ��߶���̣�֪��AP����Сֵ������ֱ��������ABCб���ϵĸߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
���ξ��ж�ƽ���ı��β����е������ǣ�������
A. ����Ա߷ֱ�ƽ�� B. ����ԽǷֱ����
C. �Խ�����ƽ�� D. �Խ����ഹֱ
D �����������������A������ȷ������Ա߷ֱ�ƽ�У� B������ȷ������ԽǷֱ���ȣ����߾��д�������ȷ���� C������ȷ���Խ�����ƽ�֣����߾����д����ʣ� D�����εĶԽ����ഹֱ��ƽ���ı���ȴ�����ʣ� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹŰ�ͷ�����꼶���£�������ѧ�Ծ� ���ͣ������
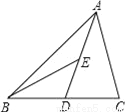
��ͼ��ABC�У�AD��BC�ϵ����ߣ�BE�ǡ�ABD��AD���ϵ����ߣ�����ABC�������24�����ABE�������__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹŰ�ͷ�����꼶���£�������ѧ�Ծ� ���ͣ���ѡ��
һ���������ع�����ʻ�����ݣ�����ͼ���д����ܷ�ӳ����������ݵ�·��S��ǧ�ף�����ʻʱ��t��Сʱ���Ĺ�ϵ���ǣ�������
A. 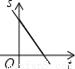 B.
B. 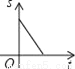 C.
C. 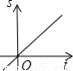 D.
D. 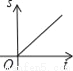
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������������2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC=8��BD=6��OE��BC������Ϊ��E����OE= ��
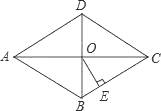
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������Դ��2016-2017ѧ���һѧ����ĩ���Ծ��꼶��ѧ�Ծ� ���ͣ������
ij��ҵ�����һ���Ʒ��ÿ���ijɱ���50Ԫ��Ϊ�˺������ۣ�Ͷ���г��������������г����飬���۵�����100Ԫʱ��ÿ�����������50���������۵���ÿ����1Ԫ��ÿ��Ϳɶ��۳�5������Ҫ�����۵��۲��õ��ڳɱ���
��1�����ÿ�����������y��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2��������۵���Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
��3���������ҵҪʹÿ�������������4000Ԫ����ÿ����ܳɱ�������7000Ԫ����ô���۵���Ӧ������ʲô��Χ�ڣ���ÿ����ܳɱ�=ÿ���ijɱ���ÿ�����������
��1��y=��5x2+800x��27500��50��x��100������2�������۵���Ϊ80Ԫʱ��y���ֵ=4500����3�����۵���Ӧ�ÿ�����82Ԫ��90Ԫ֮�䣮 ����������������� ��1���ɡ���Ʒ����=����Ʒ�ۼۡ�-����Ʒ�ɱ��ۡ��͡�������=��������Ʒ���� ����Ʒ�����������������г�������ϵʽ�� ��2���ѣ�1�������ú�������ʽ�䷽��������������Ա�����ȡֵ��Χ���Ϳ����Ա�����ȡ...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com