
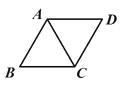
如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长是 .
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:单选题
如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为 ( )
A. –3 B. 3 C. 0 D. 1
A 【解析】(x+m)(x+3)=x2+(3+m)x+3m, 因为结果不含x的一次项,所以3+m=0,m=-3, 故选A.查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:填空题
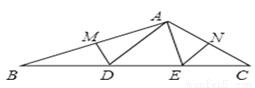
如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若△ADE的周长为20cm,则BC= cm.
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:解答题
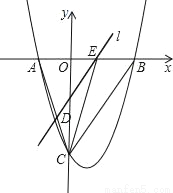
如图,抛物线y=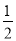 x2﹣
x2﹣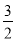 x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:解答题
先化简,再求值: 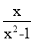 ÷(1+
÷(1+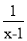 ),其中x=
),其中x=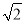 ﹣1.
﹣1.
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:单选题
在平面直角坐标系中,点P(-2,-3)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
C 【解析】试题解析:点P(-2,-3)的横坐标和纵坐标均为负数,所以点P(-2,-3) 在第三象限. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:解答题
如图①,先把一矩形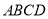 纸片上下对折,设折痕为
纸片上下对折,设折痕为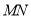 ;如图②,再把
;如图②,再把
点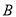 叠在折痕线
叠在折痕线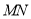 上,得到
上,得到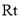
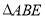 .过
.过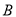 点作
点作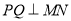 ,分别交
,分别交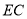 、
、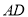 于点
于点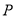 、
、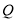 .
.
(1)求证: 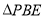 ∽
∽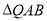 ;
;
(2)在图②中,如果沿直线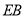 再次折叠纸片,点
再次折叠纸片,点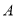 能否叠在直线
能否叠在直线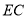 上?请说明理由;
上?请说明理由;
(3)在(2)的条件下,若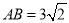 ,求
,求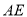 的长度.
的长度.
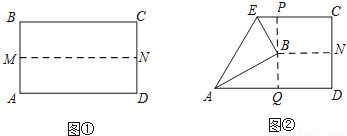
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:单选题
已知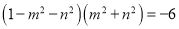 ,则m2+n2的值是( )
,则m2+n2的值是( )
A. 3 B. 3或-2 C. 2或-3 D. 2
A 【解析】, , , , ∴或(舍去), 故选A.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:填空题
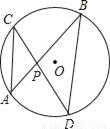
如图,在⊙O中,弦AB,CD相交于点P.若∠A=40°,∠APD=75°,则∠B= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com