练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在⊙O中，弦AB，CD相交于点P．若∠A=40°，∠APD=75°，则∠B=　 　．

    35°． 【解析】试题解析： 故答案为：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年广东省河源市中考数学一诊试卷 题型：填空题

    如图，菱形ABCD的边长为6，∠ABC=60°，则对角线AC的长是 .

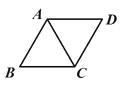
    6 【解析】试题分析：根据菱形的性质可得AB=BC=6，∵∠ABC=60°，则△ABC为等边三角形，则AC=AB=6.

    查看答案和解析>>

    科目：初中数学 来源：北京四中2018届上学期初中九年级期中考试数学试卷 题型：解答题

    抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y，的对应值如下表：

    x

    …

    -2

    -1

    0

    1

    2

    …

    y

    …

    0

    -4

    -4

    0

    8

    …

    （1）根据上表填空：

    ①抛物线与x轴的交点坐标是_________和_________；

    ②抛物线经过点（-3，_________）；

    （2）试确定抛物线y=ax2+bx+c的解析式.

    （1）①（-2，0），（1，0）；②8；（2）所求抛物线解析式为y=2x2+2x-4. 【解析】试题分析： (1)①根据表格中函数值y=0即可得到与x轴的交点坐标； ②观察表格可知抛物线的对称轴为x=,由此可知（2，8）与（-3，8）关于对称轴对称，从而可得； （2）依题意设抛物线解析式为y=a（x+2）（x-1），代入点（0，-4）即可求得. 试题解析：（1）①观察表格可...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：解答题

    如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y=ax2+bx+c过点C．动点P从点A出发，沿线段AB向点B运动．同时动点Q从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．

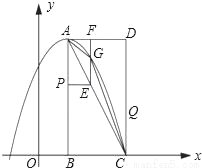
    （1）直接写出点A的坐标，并求出抛物线的解析式；

    （2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？

    （3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．

    （1）A（1，4）；y=﹣x2+2x+3；（2）当t=2时，S△ACG的最大值为1；（3）t=20﹣8 或t= ． 【解析】试题分析：（1）根据矩形的性质可以写出点A得到坐标；由顶点A的坐标可设该抛物线的顶点式方程为y=a（x-1）2+4，然后将点C的坐标代入，即可求得系数a的值（利用待定系数法求抛物线的解析式）；（2）利用待定系数法求得直线AC的方程y=-2x+6；由图形与坐标变换可以求得...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：解答题

    如图所示，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A，B的坐标分别是A（3，3）、B（1，2），△AOB绕点O逆时针旋转90°后得到△A1OB1．

    （1）画出△A1OB1，直接写出点A1，B1的坐标；

    （2）在旋转过程中，点B经过的路径的长．

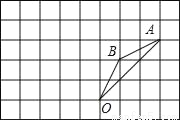
    （1）A1（﹣3，3），B1（﹣2，1）；（2） ． 【解析】试题分析：（1）根据网格结构找出点绕点逆时针旋转90°后的对应点的位置，然后顺次连接即可，再根据平面直角坐标系写出各点的坐标； （2）利用勾股定理列式求出的长，再利用弧长公式列式计算即可得解； 试题解析：（1）如图， （2）由可得：

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：填空题

    分解因式：x3-4x= ______________．

    x(x+2)(x-2) 【解析】分析：先提取公因式x，再对余下的多项式利用平方差公式继续分解． 详【解析】 x3﹣4x=x（x2﹣4）=x（x+2）（x﹣2）． 故答案为：x（x+2）（x﹣2）．

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：单选题

    下列运算正确的是（　　）

    A. 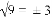B. （m2）3=m5 C. a2•a3=a5 D. （x+y）2=x2+y2

    C 【解析】A、=3，本选项错误； B、（m2）3=m6，本选项错误； C、a2•a3=a5，本选项正确； D、（x+y）2=x2+y2+2xy，本选项错误， 故选C

    查看答案和解析>>

    科目：初中数学 来源：2017年福建省分校九年级数学综合试卷（二） 题型：单选题

    2000年奥运会我国奥运健儿共夺得28枚金牌，2004年奥运会我国奥运健儿再接再厉，共取得32枚金牌，则下列说法：

    ①2004年奥运会金牌总数比2000年奥运会金牌总数增长约14.3%；

    ②2004年奥运会金牌总数比2000年奥运会金牌总数增长12.5%；

    ③若按2004年奥运会金牌总数比2000年的增长率计算，2008年北京奥运会预计我国将取得金牌总数为28（1+14.3%）2≈37枚（四舍五入取整数）；

    ④若按2004年奥运会金牌总数比2000年的增长率计算，2008年北京奥运会预计我国将取得金牌总数为32（1+12.5%）=36枚．其中正确的是（　　）

    A. ① B. ② C. ①③ D. ②④

    C 【解析】2004年奥运会金牌总数比2000年奥运会金牌总数增长率为（32﹣28）÷28=14.3%， 所以按2004年奥运会金牌总数比2000年的增长率计算， 2008年北京奥运会预计我国将取得金牌总数为28（1+14.3%）2≈37枚（四舍五入取整数）． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年黑龙江省大庆市中考数学三模试卷 题型：解答题

    先化简，再求值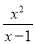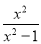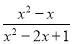：（﹣）÷，其中x是方程3x2﹣x﹣1=0的根．

    ， . 【解析】试题分析：先根据分式混合运算的法则把原式进行化简，再求出x的值，把x的值代入化简后的式子进行计算即可． 试题解析：原式=×=×=， ∵3x2﹣x﹣1=0， ∴x+1=3x2， ∴原式==．

    查看答案和解析>>

    同步练习册答案