
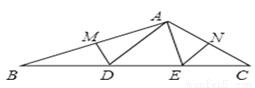
如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若△ADE的周长为20cm,则BC= cm.
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源:2016-2017学年陕西师大附中七年级(下)第一次月考数学试卷 题型:单选题
两根木棒的长度分别是5cm和7cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒的长为偶数,那么第三根木棒长的取值情况有( )
A.3种 B.4种 C.5种 D.6种
B 【解析】 试题分析:首先根据三角形的三边关系确定第三边的取值范围,再根据第三边是偶数确定其值.根据三角形的三边关系,得第三根木棒的长大于2cm而小于12cm.又第三根木棒的长是偶数,则应为4cm,6cm,8cm,10cm.查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:解答题
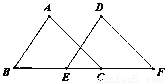
如图:点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AB∥DE.
求证:△ABC≌△DEF.
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
下列运算正确的是( )
A. 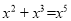 B.
B. 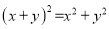 C.
C. 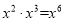 D.
D. 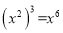
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:解答题
如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)写出A1,B1,C1的坐标,A1 ;B1 ;C1 .(直接写出答案)
(3)△A1B1C1的面积为 .(直接写出答案)
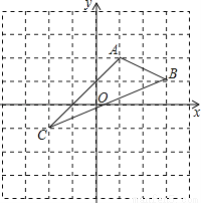
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:单选题
如图所示,△ABC为等边三角形,P为BC上一点,Q为AC上一点,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则对下面四个结论判断正确的是( )
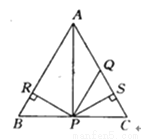
①点P在∠BAC的平分线上, ②AS=AR, ③QP∥AR, ④△BRP≌△QSP.
A. 全部正确; B. 仅①和②正确; C. 仅②③正确; D. 仅①和③正确
A 【解析】试题解析:∵PR⊥AB于R,PS⊥AC于S. ∴∠ARP=∠ASP=90°. ∵PR=PS,AP=AP. ∴Rt△ARP≌Rt△ASP. ∴AR=AS,故(2)正确,∠BAP=∠CAP. ∴AP是等边三角形的顶角的平分线,故(1)正确. ∴AP是BC边上的高和中线,即点P是BC的中点. ∵AQ=PQ. ∴点Q是AC的中点. ∴...查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:单选题
已知△ABC的三个内角满足:∠A=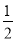 ∠B=
∠B=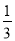 ∠C,则此三角形是( )
∠C,则此三角形是( )
A. 等腰三角形 B. 锐角三角形 C. 直角三角形 D. 钝角三角形
C 【解析】试题解析:∵∠A=∠B=∠C,. ∴∠C=3∠A,∠B=2∠A,. ∵∠A+∠B+∠C=180°,. ∴∠A+2∠A+3∠A=180°,. ∴∠A=30°,. ∴∠B=60°,∠C=90°,. ∴此三角形为直角三角形.查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:填空题
如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长是 .
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y,的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
(1)根据上表填空:
①抛物线与x轴的交点坐标是_________和_________;
②抛物线经过点(-3,_________);
(2)试确定抛物线y=ax2+bx+c的解析式.
(1)①(-2,0),(1,0);②8;(2)所求抛物线解析式为y=2x2+2x-4. 【解析】试题分析: (1)①根据表格中函数值y=0即可得到与x轴的交点坐标; ②观察表格可知抛物线的对称轴为x=,由此可知(2,8)与(-3,8)关于对称轴对称,从而可得; (2)依题意设抛物线解析式为y=a(x+2)(x-1),代入点(0,-4)即可求得. 试题解析:(1)①观察表格可...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com