练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    反比例函数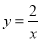的图象上有两点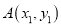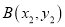， ，若x1＞x2，x1x2＞0，则y1－y2的值是（　　）

    A. 正数 B. 负数 C. 0 D. 非负数

    B 【解析】∵x1＞x2，x1x2＞0， ∴函数图像经过经过一、三象限， ∴y随x的增大而减小， ∵x1＞x2， ∴y1
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省江县初中2016年秋季八年级期末考试试卷 题型：填空题

    已知x2＋y2＝25，xy＝12，，则x＋y的值为___________

    ±7． 【解析】∵x2＋y2＝25，xy＝12， ∴（x+y）2=x2+2xy+y2=25+2×12=49， ∴x+y=±7．

    查看答案和解析>>

    科目：初中数学 来源：北京市2017-2018学年第一学期初二数学期中试卷 题型：单选题

    如图,在△ABC中,AD是它的角平分线, AB= 8cm,AC=6 cm,则= （ ）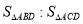

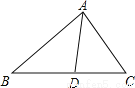
    A. 3 : 4 B. 4 : 3 C. 16 : 9 D. 9 : 16

    B 【解析】∵AD是△ABC的角平分线， ∴设△ABD的边AB上的高与△ACD的AC上的高分别为h1,h2， ∴h1=h2， ∴△ABD与△ACD的面积之比=AB:AC=8:6=4:3， 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：北京市平谷区2018届初三第一学期期末数学试卷 题型：解答题

    如图，∠ABC=∠BCD=90°，∠A=45°，∠D=30°，BC=1，AC，BD交于点O．求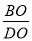的值．

    【解析】试题分析：本题考查了相似三角形的判定与性质，解直角三角形.由∠A=∠ACD，∠AOB=∠COD可证△ABO∽△CDO，从而；再在Rt△ABC和Rt△BCD中分别求出AB和CD的长，代入即可. 【解析】 ∵∠ABC=∠BCD=90°，∴AB∥CD，∴∠A=∠ACD，∴△ABO∽△CDO，∴ ． 在Rt△ABC中，∠ABC=90°，∠A=45°，BC=1，∴AB=1． 在R...

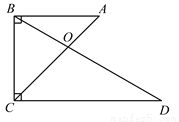
    查看答案和解析>>

    科目：初中数学 来源：北京市平谷区2018届初三第一学期期末数学试卷 题型：填空题

    已知菱形ABCD中，∠B=60°，AB=2，则菱形ABCD的面积是_________________．

    【解析】如图，作AE⊥BC于点E. ∵四边形ABCD是菱形，，AB=2， ∴BC=AB=2. ∵ , ∴AE=sin60°×2= , ∴菱形ABCD的面=BC·AE= .

    查看答案和解析>>

    科目：初中数学 来源：北京市平谷区2018届初三第一学期期末数学试卷 题型：单选题

    如图，AD∥BE∥CF，直线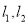与这三条平行线分别交于点A，B，C和D，E，F．已知AB=1，BC=3，DE=2，则EF的长是（　　）

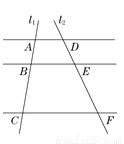
    A. 4 B. 5 C. 6 D. 8

    C 【解析】∵AD∥BE∥CF， ∴ , ∵AB=1，BC=3，DE=2， ∴ . 故选C.

    查看答案和解析>>

    科目：初中数学 来源：安徽省六安市2018届九年级上学期第二次月考数学试卷 题型：解答题

    如图，已知AB是⊙O的弦，P是AB上一点，AB=10，PA=4，OP=5，求⊙O的半径．

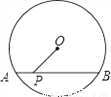
    7 【解析】试题分析：过O作OE⊥AB，垂足为E，连接OA，先求出PE的长，利用勾股定理求出OE，在Rt△AOE中，利用勾股定理即可求出OA的长． 试题解析：过O作OE⊥AB，垂足为E，连接OA， ∵AB=10，PA=4， ∴AE=AB=5，PE=AE﹣PA=5﹣4=1， 在Rt△POE中，OE===2， 在Rt△AOE中，OA===7．

    查看答案和解析>>

    科目：初中数学 来源：安徽省六安市2018届九年级上学期第二次月考数学试卷 题型：单选题

    下列各图中，是中心对称图形的是（ ）

    A. A B. B C. C D. D

    A 【解析】试题分析：根据中心对称图形的定义：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形进行解答。可知A选项是中心对称图形

    查看答案和解析>>

    科目：初中数学 来源：云南省2018届九年级上学期期中考试数学试卷 题型：单选题

    已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示，则下列结论中正确的是（　　）

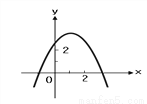
    A. abc>0 B. a+b+c>0 C. c<0 D. b<0

    B 【解析】【解析】 抛物线开口向下，则a＜0，抛物线的对称轴在y轴的右侧，则b＜0，抛物线与x轴的交点在x轴上方，则c＞0，所以A选项，C选项、D选项都错误； 由于x=1时，y＞0，即a+b+c＞0，所以B选项正确． 故选B．

    查看答案和解析>>

    同步练习册答案