
如图,圆锥体的高h=2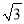 cm,底面半径r=2cm,则圆锥体的全面积为( )cm2.
cm,底面半径r=2cm,则圆锥体的全面积为( )cm2.
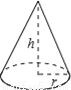
A. 4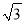 π B. 8π C. 12π D. (4
π B. 8π C. 12π D. (4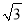 +4)π
+4)π
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(C卷) 题型:单选题
甲、乙、丙、丁四位同学的运动衫上印有不同的号码.
赵说:“甲是2号,乙是3号.”钱说:“丙是4号,乙是2号.”孙说:“丁是2号,丙是3号.”李说:“丁是4号,甲是1号.”又知道赵、钱、孙、李每人都只说对了一半,那么甲的号码是( )
A.1号 B.2号 C.3号 D.4号
B 【解析】 试题分析:找出某两个人说话的突破口,进行推理,若得出矛盾则否定之,若得不出矛盾则推理正确. 【解析】 根据赵说:“甲是2号,乙是3号.”与李说:“丁是4号,甲是1号.”假设甲既不是1号也不是2号,那么乙是3号,丁是4号,剩下的1、2号由甲与丙分,甲不是1号就是2号,这与假设相矛盾,所以假设甲既不是1号也不是2号是不正确的.假设甲是2号,那么乙不是3号,丁是4号,可...查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:填空题
某公司的年销售额为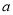 元,成本为销售额的
元,成本为销售额的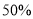 ,税额和其它费用合计为销售额为
,税额和其它费用合计为销售额为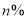 ,则用
,则用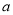 ,
, 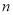 表示该公司的年利润
表示该公司的年利润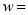 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:2017年四川省中考数学模拟试卷(3) 题型:解答题
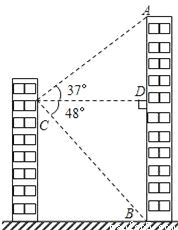
小明家所在居民楼的对面有一座大厦AB,AB=80米,为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)
(参考数据: 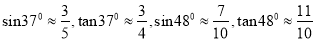 )
)
查看答案和解析>>
科目:初中数学 来源:2017年四川省中考数学模拟试卷(3) 题型:填空题
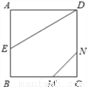
如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB,CD上滑动,当CM=_________时,△AED与以M,N,C为顶点的三角形相似.
查看答案和解析>>
科目:初中数学 来源:2017年四川省中考数学模拟试卷(3) 题型:单选题
如果-b是a的立方根,那么下列结论正确的是( ).
A. -b也是-a的立方根 B. b也是a的立方根
C. b也是-a的立方根 D. ±b都是a的立方根
C 【解析】试题分析:根据立方根的意义,可由-b是a的立方根,那么b是-a的立方根,故C正确. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(C卷) 题型:解答题
星期天,小明和小芳从同一小区门口同时出发,沿同一路线去离该小区1800米的少年宫参加活动,为响应“节能环保,绿色出行”的号召,两人都步行,已知小明的速度是小芳的速度的1.2倍,结果小明比小芳早6分钟到达,求小芳的速度.
小芳的速度是50米/分钟. 【解析】试题分析:设小芳的速度是x米/分钟,则小明的速度是1.2x米/分钟,根据路程÷速度=时间,列出方程,再求解即可. 试题解析:设小芳的速度是x米/分钟,则小明的速度是1.2x米/分钟,根据题意得: ,解得:x=50,经检验x=50是原方程的解, 答:小芳的速度是50米/分钟.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(C卷) 题型:单选题
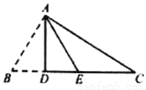
如图,在Rt△ABC中,∠BAC=90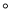 ,AD⊥BC于D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=( )
,AD⊥BC于D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=( )
A. 30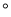 B.
B. 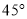 C. 60
C. 60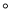 D. 75
D. 75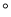
查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:填空题
在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有_____(填序号)
①②③ 【解析】∵∠A+∠B=∠C, ∠A+∠B+∠C=180°,∴2∠C=180°,∠C=90°,∴△ABC是直角三角形; ∵∠A:∠B:∠C=1:2:3,设∠A=x,则x+2x+3x=180,x=30°,∠C=30°×3=90°,∴△ABC是直角三角形; ∵∠A=90°?∠B,∴∠A+∠B=90°,则∠C=180°?90°=90°,∴△ABC是直角三角形; ∵∠A=∠B...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com