
某公司的年销售额为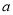 元,成本为销售额的
元,成本为销售额的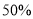 ,税额和其它费用合计为销售额为
,税额和其它费用合计为销售额为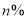 ,则用
,则用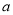 ,
, 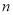 表示该公司的年利润
表示该公司的年利润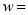 __________.
__________.
科目:初中数学 来源:山东省2017-2018学年八年级12月月考数学试卷 题型:填空题
一组数据:1,2,4,3,2,4,2,5,6,1,它们的平均数为_______,众数为_______,中位数为_______.
3 2 2.5. 【解析】根据平均数、众数与中位数的定义求解.所有数据的和除以10得平均数(1×2+2×3+3+4×2+5+6)÷10=3;将这组数据从小到大的顺序排列1,1,2,2,2,3,4,4,5,6.处于中间位置的数是2,3,那么由中位数的定义可知,这组数据的中位数是(2+3)÷2=2.5;2出现的次数最多为众数. 故答案为:3;2;2.5.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(A卷) 题型:解答题
解不等式(组)
(1)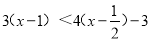 (2)
(2) (在数轴上把解集表示出来)
(在数轴上把解集表示出来)
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(A卷) 题型:单选题
下列长度(单位:cm)的三根小木棒,把它们首尾顺次相接能摆成一个三角形的是( )
A. 3,4,8 B. 8,15,7 C. 13,12,20 D. 5,5,11
C 【解析】 试题分析:三角形中任意两边之和大于第三边,任意两边之差小于第三边.查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:填空题
水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为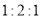 ,用两个相同的管子在容器的
,用两个相同的管子在容器的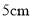 高度处连通(即管子底端离容器底
高度处连通(即管子底端离容器底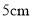 ).现三个容器中,只有甲中有水,水位高
).现三个容器中,只有甲中有水,水位高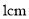 ,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水
,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水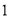 分钟,乙的水位上升
分钟,乙的水位上升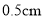 ,则开始注入__________分钟的水量后,甲与乙的水位高度之差是
,则开始注入__________分钟的水量后,甲与乙的水位高度之差是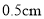 .
.

查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:单选题
在两个形状、大小完全相同的大长方形内,分别互不重叠地放入四个如图③的小长方形后得图①,图②,已知大长方形的长为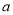 ,两个大长方形未被覆盖部分分别用阴影表示,则图①阴影部分周长与图②阴影部分周长的差是( ).
,两个大长方形未被覆盖部分分别用阴影表示,则图①阴影部分周长与图②阴影部分周长的差是( ).



A. 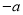 B.
B. 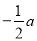 C.
C. 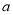 D.
D. 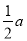
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:单选题
下列计算正确的是( ).
A. 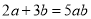 B.
B. 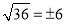 C.
C. 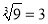 D.
D. 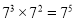
查看答案和解析>>
科目:初中数学 来源:2017年四川省中考数学模拟试卷(3) 题型:单选题
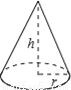
如图,圆锥体的高h=2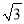 cm,底面半径r=2cm,则圆锥体的全面积为( )cm2.
cm,底面半径r=2cm,则圆锥体的全面积为( )cm2.
A. 4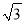 π B. 8π C. 12π D. (4
π B. 8π C. 12π D. (4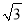 +4)π
+4)π
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题易丢分 题型:填空题
如图所示,在△ABC中,AB=6,AC=4,P是AC的中点,过P点的直线交AB于点Q,若以A、P、Q为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ的长为_____.
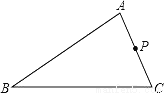
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com