
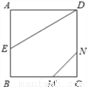
如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB,CD上滑动,当CM=_________时,△AED与以M,N,C为顶点的三角形相似.
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(C卷) 题型:填空题
点P(a+1,a﹣1)在直角坐标系的y轴上,则a= ;在第四象限内,则a的取值范围是 .
﹣1,﹣1<a<1. 【解析】 试题分析:根据点在直角坐标系的y轴上,横坐标为0,根据根据第四象限内点的横坐标是正数,纵坐标是负数列出不等式组,然后求解即可. 【解析】 ∵点P(a+1,a﹣1)在直角坐标系的y轴上, ∴a+1=0, ∴a=﹣1, ∵点P(a+1,a﹣1)在第四象限内, ∴, ∴﹣1<a<1, 则a的取值范围是﹣1<a<1, ...查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:填空题
水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为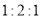 ,用两个相同的管子在容器的
,用两个相同的管子在容器的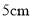 高度处连通(即管子底端离容器底
高度处连通(即管子底端离容器底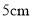 ).现三个容器中,只有甲中有水,水位高
).现三个容器中,只有甲中有水,水位高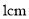 ,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水
,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水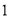 分钟,乙的水位上升
分钟,乙的水位上升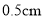 ,则开始注入__________分钟的水量后,甲与乙的水位高度之差是
,则开始注入__________分钟的水量后,甲与乙的水位高度之差是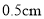 .
.

查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:单选题
下列计算正确的是( ).
A. 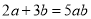 B.
B. 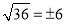 C.
C. 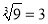 D.
D. 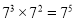
查看答案和解析>>
科目:初中数学 来源:2017年四川省中考数学模拟试卷(3) 题型:解答题
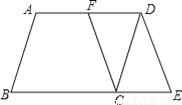
如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=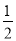 BC,连接DE,CF.
BC,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源:2017年四川省中考数学模拟试卷(3) 题型:单选题
如图,圆锥体的高h=2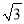 cm,底面半径r=2cm,则圆锥体的全面积为( )cm2.
cm,底面半径r=2cm,则圆锥体的全面积为( )cm2.
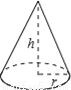
A. 4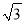 π B. 8π C. 12π D. (4
π B. 8π C. 12π D. (4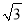 +4)π
+4)π
查看答案和解析>>
科目:初中数学 来源:2017年四川省中考数学模拟试卷(3) 题型:单选题
下列计算正确的是( )
A. 3a+4b=7ab B. (ab3)2=ab6 C. (a+2)2=a2+4 D. x12÷x6=x6
D 【解析】试题分析:选项A,3a与4b不是同类项,不能合并,故选项A错误;选项B,(ab3)3=ab9,故选项B错误;选项C,(a+2)2=a2+4a+4, 故选项C错误;选项x12÷x6=x12-6=x6,正确,故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(C卷) 题型:填空题
把多项式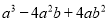 分解因式的结果是_______________.
分解因式的结果是_______________.
查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:解答题
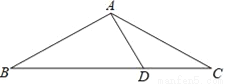
如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com