练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知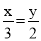： ，那么下列式子中一定成立的是（　　）

    A. 2x=3y B. 3x=2y C. x=6y D. xy=6

    A 【解析】∵ ， ∴2x=3y. 故选A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省苏州市2017年中考二模试卷数学试卷 题型：单选题

    已知关于x的方程mx+3=4的解为x=1，则直线y=（m﹣2）x﹣3一定不经过的象限是（   ）

    A. 第一象限                            B. 第二象限                            C. 第三象限                            D. 第四象限

    A 【解析】试题分析：∵关于x的方程mx＋3＝4的解为x＝1， ∴m＋3＝4， ∴m＝1， ∴直线y＝(m－2)x－3为直线y＝－x－3， ∴直线y＝(m－2)x－3一定不经过第一象限， 故选A．

    查看答案和解析>>

    科目：初中数学 来源：重庆市秀山县2017-2018学年七年级上学期八校联考数学试卷 题型：填空题

    已知多项式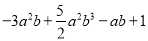，则这个多项式的次数是______ ．

    5 【解析】由多项式的次数是这个多项式中此时最高的项的次数可知：多项式的次数是. 即答案为：5.

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：解答题

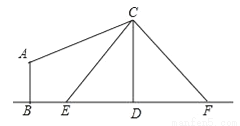
    如图，电线杆CD上的C处引拉线CE，CF固定电线杆，在离电线杆6米的B处安置测角仪（点B，E，D在同一直线上），在A处测得电线杆上C处的仰角为30°，已知测角仪的高AB=1.5米，BE=2.3米，求拉线CE的长，（精确到0.1米）参考数据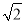≈1.41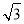，≈1.73．

    6.2． 【解析】 试题分析：过点A作AM⊥CD于点M，可得四边形ABDM为矩形，根据A处测得电线杆上C处得仰角为23°，在△ACM中求出CM的长度，然后在Rt△CDE中求出CE的长度． 试题解析：过点A作AM⊥CD于点M，则 四边形ABDM为矩形，AM=BD=6米，在Rt△ACM中，∵∠CAM=30°，AM=6米，∴CM=AM•tan∠CAM=6×=（米），∴CD=+1....

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：填空题

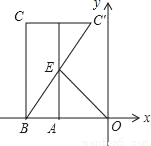
    如图，已知点A的坐标为（m，0），点B的坐标为（m﹣2，0），在x轴上方取点C，使CB⊥x轴，且CB=2AO，点C，C′关于直线x=m对称，BC′交直线x=m于点E，若△BOE的面积为4，则点E的坐标为_____．

    （﹣2，2） 【解析】如图,设AE与CC′交于点D. ∵点A的坐标为(m,0)，在x轴上方取点C，使CB⊥x轴，且CB=2AO， ∴CB=?2m. ∵点C,C′关于直线x=m对称， ∴CD=C′D， ∵ABCD是矩形，AB=CD， ∴AB=C′D. 又∵∠BAE=∠C′DE=90°,∠AEB=...

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：单选题

    如图，过反比例函数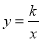（x＞0）的图象上一点A作AB⊥x轴于点B，连接AO，若S△AOB=2，则k的值为（ ）

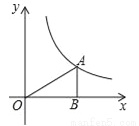
    A. 2 B. 3 C. 4 D. 5

    C 【解析】试题分析：∵点A是反比例函数图象上一点，且AB⊥x轴于点B，∴S△AOB=|k|=2，解得：k=±4． ∵反比例函数在第一象限有图象，∴k=4．故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：单选题

    分式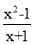的值为零，则x的值为（　　）

    A. ﹣1 B. 0 C. ±1 D. 1

    D 【解析】由题意得 解之得 x=1. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古鄂尔多斯市鄂托克旗八年级（下）期末数学试卷 题型：单选题

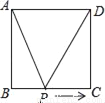
    如图，正方形ABCD的边长为2cm，动点P从点A出发，在正方形的边上沿A→B→C的方向运动到点C停止，设点P的运动路程为x（cm）在下列图象中，表示△ADP的面积y（cm2）关于x（cm）的函数关系的图象是（　　）

    A. B. C. D.

    A 【解析】【解析】 当P点由A运动到B点时，即0≤x≤2时，y=×2x=x，当P点由B运动到C点时，即2＜x＜4时，y=×2×2=2，符合题意的函数关系的图象是A；故选A．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型：填空题

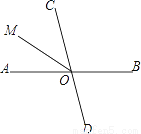
    如图，直线AB，CD交于点O，射线OM平分∠AOC，若∠AOC=76°，则∠BOM=________．

    142° 【解析】因为∠AOC=76°, 射线OM平分∠AOC,所以∠AOM=76°÷2=38°, 所以∠BOM=180°－∠AOM=180°－38°=142°,故答案为: 142°.

    查看答案和解析>>

    同步练习册答案