
已知关于x的一元二次方程ax2﹣2x﹣1=0有两个不相等的实数根,则a的取值范围是__________
a>﹣1且a≠0 【解析】∵关于的一元二次方程有两个不相等的实数根, ∴ ,解得: 且. 即的取值范围是: 且. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:安徽省合肥市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型:单选题
如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
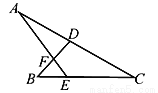
A. 120° B. 115° C. 110° D. 105°
C 【解析】试题分析:因为∠A=27°,∠C=38°,所以∠AEB=∠A+∠C=65°,又因∠B=45°,所以∠DFE=∠B+∠AEB=110°,故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年内蒙古乌兰察布市分校九年级(上)期中数学试卷 题型:填空题
如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB=______°.
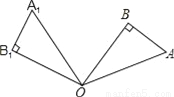
查看答案和解析>>
科目:初中数学 来源:甘肃省白银市2018届九年级(上)期中数学试卷 题型:解答题
利用一面墙(墙的长度不限),另三边用58m长的篱笆围成一个面积为200m2的矩形场地,求矩形的长和宽.
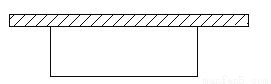
查看答案和解析>>
科目:初中数学 来源:甘肃省白银市2018届九年级(上)期中数学试卷 题型:填空题
已知实数m,n满足3m2+6m﹣7=0,3n2+6n﹣7=0,且m≠n,则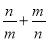 =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源:甘肃省白银市2018届九年级(上)期中数学试卷 题型:单选题
若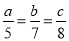 ,且
,且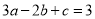 ,则
,则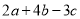 的值为:
的值为:
A. 14 B. 42 C. 7 D. 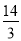
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古包头市七年级(下)期中数学试卷 题型:解答题
如图,已知△ABC中,AB=6cm,∠B=∠C,BC=4cm,点D为AB的中点.若点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?

查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古包头市七年级(下)期中数学试卷 题型:单选题
三角形两边长分别为3和5,若第三边的长为偶数,则这个三角形的周长可能是( )
A. 10或12 B. 10或14 C. 12或14 D. 14或16
C 【解析】【解析】 设三角形第三边的长为a,∵三角形的两边长分别为3和5,∴5﹣3<a<5+3,即2<a<8,∵a为偶数,∴a=4或a=6,当a=4时,这个三角形的周长=3+4+5=12; 当a=6时,这个三角形的周长=3+5+6=14. 综上所述,这个三角形的周长可能是12或14. 故选C.查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古包头市八年级(下)期中数学试卷 题型:填空题
如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为 .
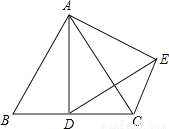
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com