
把函数y=﹣2x2的图象向左平移1个单位,再向上平移6个单位,所得的抛物线的函数关系式是( )
A. y=﹣2(x﹣1)2+6 B. y=﹣2(x﹣1)2﹣6 C. y=﹣2(x+1)2+6 D. y=﹣2(x+1)2﹣6
C 【解析】原抛物线的顶点坐标为(1,3),向左平移2个单位,再向上平移3个单位得到新抛物线的顶点坐标为(?1,6).可设新抛物线的解析式为:y=?2(x?h) ²+k,代入得:y=?2(x+1) ²+6. 故选C.科目:初中数学 来源:甘肃省平凉市崆峒区2017-2018学年度第一学期期末数学试卷及答案 题型:解答题
先化简,再求值: 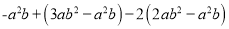 ,其中
,其中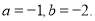
查看答案和解析>>
科目:初中数学 来源:四川省西昌市2017-2018学年九年级数学(上)期末模拟试卷 题型:填空题
一元二次方程x2=x的解为_____.
x1=0,x2=1 【解析】试题分析:首先把x移项,再把方程的左面分解因式,即可得到答案. 试题解析:移项得:x2-x=0, ∴x(x-1)=0, x=0或x-1=0, ∴x1=0,x2=1.查看答案和解析>>
科目:初中数学 来源:重庆市2018届2017年秋期期末冲刺卷 题型:填空题
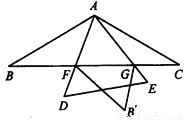
如图, 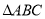 中,
中, 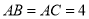 ,
, 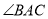 =120°,以
=120°,以 为一个顶点的等边三角形
为一个顶点的等边三角形 绕点A在
绕点A在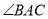 内旋转,
内旋转, 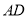 、
、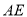 所在的直线与
所在的直线与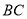 边分别交于点
边分别交于点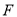 、
、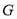 ,若点
,若点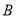 关于直线
关于直线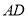 的对称点为
的对称点为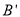 ,当
,当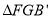 是以点
是以点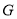 为直角顶点的直角三角形时,
为直角顶点的直角三角形时, 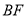 的长为__
的长为__
查看答案和解析>>
科目:初中数学 来源:重庆市2018届2017年秋期期末冲刺卷 题型:单选题
如图,一圆内切于四边形ABCD,AB=16,CD=10,则四边形ABCD的周长为( )
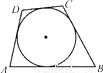
A. 50 B. 52 C. 54 D. 56
B 【解析】试题解析:根据切线长定理,可以证明圆外切四边形的性质:圆外切四边形的两组对边的和相等, 所以四边形的周长为: 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初一上期中数学试卷数学试卷 题型:解答题
阅读题:我们把能够化成分数形式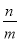 (
(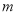 、
、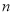 是整数,
是整数, 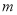 不等于
不等于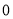 )的数叫做有理数.无限循环小数也是有理数,那它是怎么化成
)的数叫做有理数.无限循环小数也是有理数,那它是怎么化成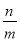 (
(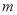 、
、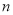 是整数,
是整数, 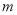 不等于
不等于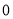 )的呢?请看下面的方法.
)的呢?请看下面的方法.
例:化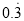 为分数.
为分数.
设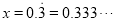 ①
①
则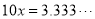 ②
②
则由① ②得,
②得, 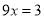 ,即
,即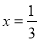 ,
, 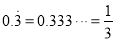
根据材料,完成下面的问题
( )根据上述提供的方法把
)根据上述提供的方法把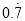 化为分数,则
化为分数,则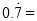 __________.
__________.
(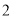 )根据上述提供的方法把
)根据上述提供的方法把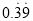 化为分数,写出过程.
化为分数,写出过程.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初一上期中数学试卷数学试卷 题型:填空题
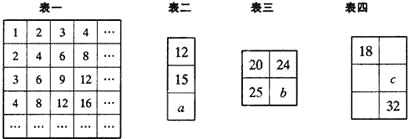
观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a+b+c的值为 .
查看答案和解析>>
科目:初中数学 来源:广东省广州市越秀区2016-2017学年八年级下册数学期末考试试卷 题型:解答题
下面我们做一次折叠活动:
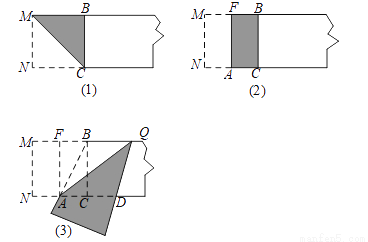
第一步,在一张宽为2的矩形纸片的一端,利用图(1)的方法折出一个正方形,然后把纸片展平,折痕为MC;
第二步,如图(2),把这个正方形折成两个相等的矩形,再把纸片展平,折痕为FA;
第三步,折出内侧矩形FACB的对角线AB,并将AB折到图(3)中所示的AD处,折痕为AQ.
根据以上的操作过程,完成下列问题:
(1)求CD的长.
(2)请判断四边形ABQD的形状,并说明你的理由.
(1);(2)四边形ABQD是菱形. 【解析】试题分析:(1)首先证明四边形MNCB为正方形,然后再依据折叠的性质得到:CA=1,AB=AD,最后再依据CD=AD-AC求解即可; (2)根据平行线的性质和折叠的性质可得到∠BAQ=∠BQA,然后依据等角对等边的性质得到AB=BQ,接下来,依据一组对边平行且相等的四边形为平行四边形可证明四边形ABQD是平行四边形,再由AB=AD,可得四边...查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试七年级数学试卷 题型:单选题
已知点C是线段AB上的一点,不能确定点C是AB中点的条件是:
A. AC=CB B. AC=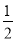 AB C. AB=2BC D. AC+CB=AB
AB C. AB=2BC D. AC+CB=AB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com