
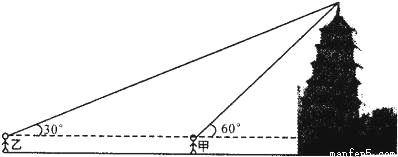
又到了一年中的春游季节,某班学生利用周末到白塔山去参观“晏阳初博物馆”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.5m;
乙:我们相距20m.
请你根据两位同学的对话,计算白塔的高度.(精确到1米)
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:填空题
分解因式:(a2+1)2﹣4a2=_____.
(a+1)2(a﹣1)2 【解析】分析:本题利用平方差公式进行因式分解即可. 解析:原式= . 故答案为(a+1)2(a﹣1)2查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷(三) 题型:解答题
A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B、C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
(1);(2) . 【解析】试题分析:(1)直接列举出两次传球的所有结果,球球恰在B手中的结果只有一种即可求概率;(2)画出树状图,表示出三次传球的所有结果,三次传球后,球恰在A手中的结果有2种,即可求出三次传球后,球恰在A手中的概率. 试题解析: 【解析】 (1)两次传球的所有结果有4种,分别是A→B→C,A→B→A,A→C→B,A→C→A.每种结果发生的可能性相等,球球恰在...查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷(三) 题型:单选题
如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若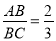 ,DE=4,则EF的长是( )
,DE=4,则EF的长是( )
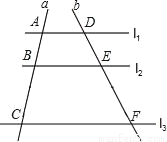
A. 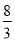 B.
B. 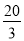 C. 6 D. 10
C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学模拟试卷 题型:解答题
已知二次函数y=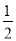 x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,顶点为P.
x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,顶点为P.
(1)求这个二次函数的解析式,并在下面的坐标系中画出该二次函数的图象;
(2)设D为线段OC上的一点,满足∠DPC=∠BAC,求点D的坐标;
(3)在x轴上是否存在一点M,使以M为圆心的圆与AC、PC所在的直线及y轴都相切?如果存在,请求出点M的坐标;若不存在,请说明理由.
(1)y=x2﹣x﹣; P(1,﹣2),C(3,0)(2)D(,0)(3)存在 【解析】试题分析:(1)利用待定系数法求出的值后可求出该函数的解析式; (2)证明利用线段比求出各相关线段的值后易求点的坐标; (3)过M作MH⊥AC,MG⊥PC垂足分别为H、G,推出是等腰直角三角形,M是的内切圆圆心,根据直线与圆的关系进行解答. 试题解析:(1)∵二次函数的图象过点A(?3,6),B...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学模拟试卷 题型:填空题
如图,Rt△ABC的斜边AB在直线l上,AC=1,AB=2.将Rt△ABC绕点B在平面内按顺时针方向旋转,使边BC落在直线l上,得到△A1BC1,再将△A1BC1绕点C1在平面内按顺时针方向旋转,使边A1C1落到直线l上,得到△A2B1C1,则点A所经过的两条弧的长度和为_____.
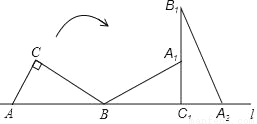
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学模拟试卷 题型:单选题
一个圆锥形的零件,如果经过圆锥的轴的剖面是一个边长为4cm的等边三角形,那么圆锥的表面积是( )
A. 8πcm2 B. 10πcm2 C. 12πcm2 D. 16πcm2
C 【解析】试题解析:圆锥的轴的剖面是一个边长为4cm的等边三角形,则底面半径=2cm,底面周长=4πcm, 底面面积= 侧面面积 ∴圆锥的表面积 故选C.查看答案和解析>>
科目:初中数学 来源:2017年天津109中中考数学模拟试卷 题型:填空题
如图,在平面直角坐标系中,抛物线y=a1(x﹣2)2+2与y=a2(x﹣2)2﹣3的顶点分别为A,B,与x轴分别交于点O,C,D,E.若点D的坐标为(﹣1,0),则△ADE与△BOC的面积比为______.
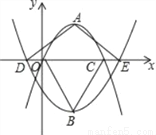
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
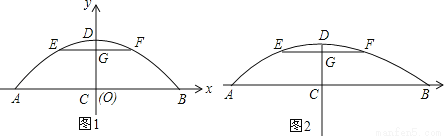
一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系.
①求抛物线的解析式;
②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分.
①求圆的半径;
②要使高为3米的船通过,则其宽度须不超过多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com