练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算：

    1. 【解析】根据绝对值、算术平方根、幂的性质计算。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：初一数学第一学期5.2.3去分母解一元一次方程 同步练习 题型：单选题

    解方程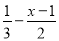=1,去分母正确的是(　)

    A. 1-(x-1)=1 B. 2-3(x-1)=6

    C. 2-3(x-1)=1 D. 3-2(x-1)=6

    B 【解析】去分母的方法是方程左右两边同时乘以分母的最小公倍数，注意不能漏乘． 【解析】 方程左右两边同时乘以6 得：2﹣3（x﹣1）=6． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：单选题

    一艘轮船和一艘渔船同时沿各自的航向从港口O出发，如图所示，轮船从港口O沿北偏西20°的方向行60海里到达点M处，同一时刻渔船已航行到与港口O相距80海里的点N处，若M、N两点相距100海里，则∠NOF的度数为（ ）

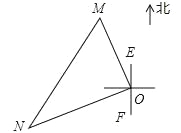
    A. 50° B. 60° C. 70° D. 80°

    C 【解析】试题分析：∵OM=60海里，ON=80海里，MN=100海里，∴OM2+ON2=MN2，∴∠MON=90°，∵∠EOM=20°，∴∠NOF=180°﹣20°﹣90°=70°．故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级上册4.7三角形相似专题--高的比等于相似比 题型：解答题

    如图，在△ABC中，DE∥BC，△ABC的高AM交DE于点N，BC=15，AM=10，DE=MN，求MN的长．

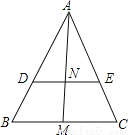
    6 【解析】 试题分析：设MN=x，则AN=10﹣x，由平行线分线段成比例定理得出比例式，即可得出MN的长． 【解析】 设MN=x，则AN=10﹣x， ∵DE∥BC， ∴， 即， 即MN的长为6．

    查看答案和解析>>

    科目：初中数学 来源：广东省2017届九年级上学期第二次月考数学试卷 题型：解答题

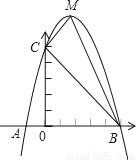
    已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．

    （1）求抛物线的解析式；

    （2）求△MCB的面积S△MCB．

    （1）抛物线的解析式为y=﹣x2+4x+5；（2）S△MCB= 15． 【解析】试题分析：（1）把A（﹣1，0）、C（0，5）、点（1，8）分别代入y=ax2+bx+c，得方程组，解方程组求得a、b、c的值，即可得抛物线的解析式；（2）利用函数的解析式求得点B、点M的坐标，作ME⊥y轴于点E，利用S△MCB=S梯形MEOB﹣S△MCE﹣S△OBC即可求得△MCB的面积． （1）依题意：...

    查看答案和解析>>

    科目：初中数学 来源：广东省2017届九年级上学期第二次月考数学试卷 题型：填空题

    分解因式：a2b﹣2ab+b=_______．

    b（a﹣1）2 【解析】先提取公因式b，再利用完全平方公式进行二次分解． 【解析】 a2b﹣2ab+b， =b（a2﹣2a+1），（提取公因式） =b（a﹣1）2．（完全平方公式）

    查看答案和解析>>

    科目：初中数学 来源：广东省2017届九年级上学期第二次月考数学试卷 题型：单选题

    将二次函数y=2（x﹣1）2﹣3的图象向右平移3个单位，则平移后的二次函数的顶点是（　　）

    A. （﹣2，﹣3） B. （4，3） C. （4，﹣3） D. （1，0）

    C 【解析】试题分析：图像向右平移3个单位，对称轴也向右平移3个单位，顶点的横坐标向右平移三个单位，纵坐标不变，故顶点坐标变为（4，﹣3），故选C.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 第24章小结与复习 练习 题型：填空题

    在周长为26π的⊙O 中,CD 是⊙O 的一条弦,AB 是⊙O 的切线,且 AB∥CD，若 AB 和CD 之间的距离为18，则弦CD 的长为 ．

    24 【解析】试题解析：如图，设AB与O相切于点F，连接OF，OD，延长FO交CD于点E. ∵2πR=26π， ∴R=13， ∴OF=OD=13， ∵AB是O切线， ∴OF⊥AB， ∴EF⊥CD即OE⊥CD， ∴CE=ED， ∵EF=18，OF=13， ∴OE=5， 在RT△OED中, ∴CD=2ED=24. 故答案为2...

    查看答案和解析>>

    科目：初中数学 来源：《概率的进一步认识》单元测试2 题型：填空题

    在中考体育达标跳绳项目测试中，1分钟跳160次为达标，小敏记录了他预测时1分钟跳的次数分别为145,155,140,162,164，则他在该次预测中达标的概率是___。

    0.4 【解析】试题分析：概率的求法：概率=所求情况数与所有情况数的比. 由题意得他在该次预测中达标的概率是2÷5=0.4.

    查看答案和解析>>

    同步练习册答案