
抛物线y=(x-2)2+1的顶点坐标是__________.
(2,1) 【解析】∵顶点式y=a(x-h)2 +k,顶点坐标是(h,k), ∴抛物线y=(x-2)2+1的顶点坐标是(2,1), 故答案为:(2,1).科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:单选题
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图1),把余下的部分拼成一个矩形(如图2),根据两个图形中阴影部分的面积相等,可以验证( )
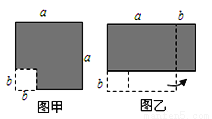
A. 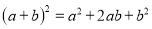 B.
B. 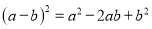
C. 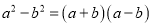 D.
D. 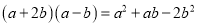
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:填空题
已知三条线段的长分别为1cm,2cm, 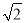 cm,如果另外一条线段与它们是成比例线段,则另外一条线段的长为__________________.
cm,如果另外一条线段与它们是成比例线段,则另外一条线段的长为__________________.
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
青青书店购进了一批进价为每本20元的中华传统文化丛书. 在销售的过程中发现,这种图书每天的销售数量y(本)与销售单价x(元)满足一次函数关系:y=-3x+108(20<x<36). 如果销售这种图书每天的利润为p(元),那么销售单价定为多少元时,每天获得的利润最大?最大利润是多少?
销售单价定为28元时,每天获得的利润最大,最大利润是192元. 【解析】试题分析:由利润=每本书的利润×数量就可以得出解析式,再根据函数的性质即可得到最大利润. 试题解析:p=(x-20)(-3x+108)=-3x2+168x-2160=-3(x-28)2+192, ∵20查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
如图,△ABC中,D、E分别是AB、AC上的点,且满足AB·AD=AE·AC,连接DE. 求证:∠ABC=∠AED.
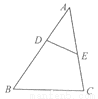
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:单选题
若A(1,y1),B(2,y2)两点都在反比例函数y=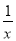 的图象上,则y1与y2的大小关系是( ).
的图象上,则y1与y2的大小关系是( ).
A. y1< y2 B. y1= y2 C. y1> y2 D. 无法确定
C 【解析】∵A(1,y1),B(2,y2)两点都在反比例函数y=的图象上, ∴1? y1=1,2? y2=1, 解得:y1=1, y2=, ∵1>, ∴y1>y2. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:解答题
如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数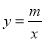 的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,﹣1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,﹣1),DE=3.
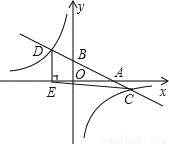
(1)求反比例函数与一次函数的解析式;
(2)求△CDE的面积.
(1)y=﹣,y=﹣x+2;(2)12. 【解析】试题分析: 分析题意,已知点在反比例函数的图象上,将点坐标代入反比例函数的解析式中即可得到的值,再由的长度求出点D的坐标;把两点的坐标代入一次函数即可求得一次函数的解析式. 过C作CH⊥轴于点H,根据 S△CDE=S△CAE+S△DAE,即可求出面积. 试题解析:(1)∵点在反比例图象上, ∴将代入反比例解析式得: 即 ...查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:单选题
已知点A,B分别在反比例函数y=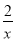 (x>0),y=
(x>0),y=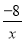 (x>0)的图象上且OA⊥OB,则tanB为( )
(x>0)的图象上且OA⊥OB,则tanB为( )
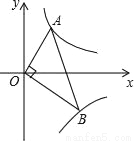
A. 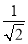 B.
B. 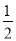 C.
C. 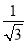 D.
D. 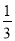
查看答案和解析>>
科目:初中数学 来源:2017年湖北省随州市中考数学模拟试卷 题型:填空题
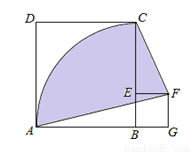
如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画圆,连结AF,CF,则图中阴影部分面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com