练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一个三角形的三个内角的度数比是1：2：1，这个三角形是（　　）．

    A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰直角三角形

    D 【解析】【解析】 最大内角=180°×=90°，另外内角=180°×=45°．故三角形为等腰直角三角形．故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：黑龙江省大庆市（五四制）2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

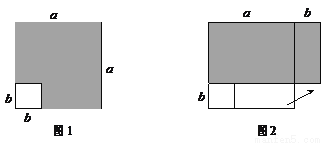
    在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图1），把余下的部分拼成一个矩形（如图2），根据两个图形中阴影部分的面积相等，可以验证（   ）

    A.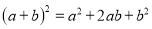

    B.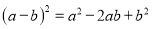

    C.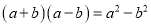

    D.

    C 【解析】∵图甲中阴影部分的面积=a2?b2，图乙中阴影部分的面积=(a+b)(a?b)， 而两个图形中阴影部分的面积相等， ∴a2?b2=(a+b)(a?b). 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：陕西省2016-2017学年八年级下学期期末考试数学试卷 题型：填空题

    分解因式： __________．

    【解析】原式= =.

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型：填空题

    如图，点B，C，E，F在同一直线上，AB∥DC，DE∥GF，∠B=∠F=72°，则∠D=________．

    36° 【解析】根据两直线平行，同位角相等可得∠DCE=∠B，∠DEC=∠F，再利用三角形的内角和定理列式计算即可得解． 【解析】 ∵AB∥DC，DE∥GF，∠B=∠F=72°， ∴∠DCE=∠B=72°，∠DEC=∠F=72°， 在△CDE中，∠D=180°﹣∠DCE﹣∠DEC=180°﹣72°﹣72°=36°． 故答案为：36．

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型：解答题

    如图，将三角尺的直角顶点放在直线a上，a∥b，∠1=50°，∠2=60°，求∠3的度数．

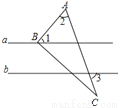
    70°． 【解析】 试题分析：本题考查的是平行线的性质，三角形的内角和定理，掌握两直线平行，同位角相等是解决问题的前提．先根据三角形内角和定理求出∠4的度数，由对顶角相等求出∠5的度数，根据平行线的性质即可得出结论． 试题解析： 如图， ∵△BCD中，∠1=50°，∠2=60°， ∴∠4=180°﹣∠1﹣∠2=180°﹣50°﹣60°=70°， ∴∠5=∠...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 测试 题型：解答题

    如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图．

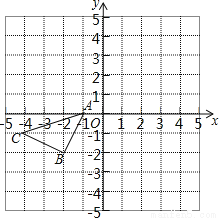
    （1）将△ABC向右平移1个单位长度，再向上平移4个单位长度，请画出平移后的△A1B1C1．

    （2）画出△ABC关于坐标原点O成中心对称的△A2B2C2．

    见解析 【解析】 试题分析：（1）直接利用平移的性质得出各点坐标，进而得出答案； （2）直接利用关于原点对称点的性质得出各点坐标，进而得出答案． 【解析】 （1）如图所示：△A1B1C1，即为所求； （2）如图所示：△A2B2C2，即为所求．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 测试 题型：单选题

    已知点P（2+m，n﹣3）与点Q（m，1+n）关于原点对称，则m﹣n的值是（ ）

    A．1 B．﹣1 C．2 D．﹣2

    D 【解析】 试题分析：根据关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，可得m、n的值，根据有理数的减法，可得答案． 【解析】 由点P（2+m，n﹣3）与点Q（m，1+n）关于原点对称，得 2+m+m=0，n﹣3+1+n=0． 解得m=﹣1，n=1． m﹣n=﹣1﹣1=﹣2， 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型：单选题

    如果一个多边形的边数增加1，那么它的内角和增加( )．

    A. 0° B. 90° C. 180° D. 360°

    C 【解析】【解析】 设原多边形边数是n，则n边形的内角和是（n-2）•180°，边数增加1，则新多边形的内角和是（n+1-2）•180°．则（n+1-2）•180°-（n-2）•180°=180°．故它的内角和增加180°．故选C．

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市2018届九年级上学期期中考试数学试卷 题型：填空题

    已知一个正六边形的边心距为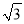，则它的半径为______ ．

    2 【解析】试题分析：设正六边形的中心是O，一边是AB，过O作OG⊥AB与G，在直角△OAG中，根据三角函数即可求得OA． 【解析】 如图所示, 在Rt△AOG中,OG=,∠AOG=30°， ∴OA=OG÷cos 30°=÷=2； 故答案为：2.

    查看答案和解析>>

    同步练习册答案