
如图,?ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB= ,AC=2,BD=4,则AE的长为( )
,AC=2,BD=4,则AE的长为( )

A.  B.
B.  C.
C.  D.
D. 
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源:黑龙江省安达市2017-2018学年七年级上学期期末质量检测数学试卷 题型:填空题
将有理数0.23456精确到百分位的结果是___________.
0.23 【解析】精确到百分位就是把千分位上的数字4进行四舍五入,故0.23456精确到百分位的结果是0.23. 故答案为:0.23查看答案和解析>>
科目:初中数学 来源:山西大学附中2018届九年级10月月考数学试卷 题型:填空题
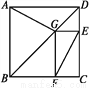
如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1 500 m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3 100 m,则小聪行走的路程为 m.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:解答题
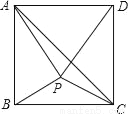
如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
求证:(1)△APB≌△DPC;(2)∠BAP=2∠PAC.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:填空题
我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 尺.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:单选题
已知三角形三条边分别是1, 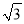 ,2,则该三角形为( )
,2,则该三角形为( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 无法确定
B 【解析】因为 ,根据勾股定理的逆定理可得该三角形为直角三角形,故选B.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
先化简,  ,并任选一个你喜欢的数
,并任选一个你喜欢的数 代入求值.
代入求值.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
医学研究发现一种新病毒的直径约为0.000043毫米,这个数用科学记数法表为( )
A. 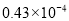 B.
B. 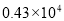 C.
C. 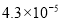 D.
D. 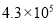
查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:单选题
如图,在五边形ABCDE中,AB=AC=AD=AE, 且AB∥ED,∠AED=70°,则∠DCB=( )
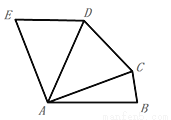
A. 70° B. 165° C. 155° D. 145°
D 【解析】∵AB∥ED, ∴∠EAB+∠AED=180°, ∵∠AED=70°, ∴∠EAB=110°, ∵AD=AE,∠AED=70°, ∴∠DAE=40°, ∴∠BAD=∠EAB -∠DAE=70°, 在四边形ABCD中,∠BAD+∠ABC+∠BCD+∠ADC=360°, ∴∠ABC+∠BCD+∠ADC=290°, ∵AB=AC=A...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com