练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    平面直角坐标系内，点P（3，-4）到y轴的距离是 _______________

    3 【解析】根据平面直角坐标系的特点，可知到y轴的距离为横坐标的绝对值，因此可知P点到y轴的距离为3. 故答案为：3.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册 第6章 数据的收集与整理 单元题测试 题型：单选题

    某次考试中，某班级的数学成绩被绘制成了如图所示的频数分布直方图．下列说法错误的是( )

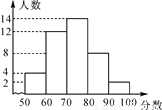
    A. 得分在70～80分之间的人数最多 B. 该班的总人数为40

    C. 得分在90～100分之间的人数占总人数的5% D. 及格(不低于60分)的人数为26

    D 【解析】根据图形得:50～60分之间的人数为4人,60～70分之间的人数为12人,70～80分之间的人数为14人,80～90分之间的人数为8人,90～100分之间的人数为2人,则得分在70～80分之间的人数最多,得分在90～100分之间的人数最少,总人数为4+12+14+8+2=40人,不低于60分为及格,该班的及格率为（12+14+8+2）÷40=90%,故选D．

    查看答案和解析>>

    科目：初中数学 来源：山东省临沂市经济开发区2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    （1）因式分【解析】
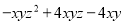    （2）因式分解：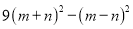

    （3）解方程：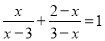

    （1）；（2）；（3）. 【解析】试题分析： 提取公因式法和公式法相结合. 运用平方差公式进行因式分解. 按照解分式方程的步骤解方程即可. 试题解析： （1）， （2） （3）两边乘,得到， ， ， 检验：当时， ， 故是分式方程的根.

    查看答案和解析>>

    科目：初中数学 来源：山东省临沂市经济开发区2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    一个三角形的两边长为3和7，第三边长为偶数，则第三边为（   ）

    A. 6 B. 6或8 C. 4 D. 4或6

    B 【解析】试题解析：设第三边为x， 则7?3

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册第七章7.1《平面直角坐标系》同步练习数学试卷 题型：解答题

    已知A(a－3，a2－4)，求a的值及点A的坐标．

    (1)当点A在x轴上；

    (2)当点A在y轴上．

    (1) a＝±2，点A的坐标为(－1，0)或(－5，0);(2) a＝3，点A的坐标为(0，5)． 【解析】试题分析：（1）根据点在x轴上时，纵坐标为0，求出a的值，进而求出点A的坐标； （2）根据点在y轴上时，横坐标为0，求出a的值，进而求出点A的坐标. 试题解析：(1)∵A在x轴上， ∴a2－4＝0，即a＝±2， ∴a－3＝－1或－5， ∴点A的坐标为(－1...

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册第七章7.1《平面直角坐标系》同步练习数学试卷 题型：单选题

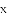
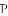
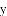
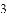
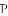
    若轴上点到轴的距离为，则点为（ ）

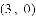
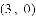
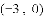
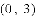
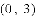
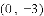
    A. B. 或 C. D. 或

    B 【解析】【解析】 设P的坐标为(a,b), ∵点P在x轴上且到轴的距离为, ∴b=0,|a|=3,即a=3或a=-3、b=0, ∴点P的坐标为或， 故选B。

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学第20章数据的分析单元检测卷 题型：解答题

    某酒店共有6名员工，所有员工的工资如下表所示：

    人  员

    经理

    会计

    厨师

    服务员1

    服务员2

    勤杂工

    月工资（元）

    6000

    3000

    4000

    2000

    2000

    1000

    （1）酒店所有员工的平均月工资是多少元？中位数、众数各是多少？

    （2）平均月工资能准确反映该酒店员工工资的一般水平吗？若能，请说明理由．若不能，如何才能较准确地反映该酒店员工工资的一般水平？谈谈你的看法．

    （1）平均月工3000（元），众数为2000元，中位数2500元； （2）这组数据的众数是2000元，才能较准确地反映该酒店员工工资的一般水平，原因是它符合多数人的工资水平． 【解析】试题分析：（1）根据平均数的计算公式，直接求出酒店所有员工的平均月工资即可； （2）由平均数的值，可见平均月工资不能准确反映该酒店员工工资的一般水平，反映该酒店员工工资的一般水平的统计量应符合多数人...

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学第20章数据的分析单元检测卷 题型：单选题

    某一公司共有51名员工（其中包括1名经理），经理的工资高于其他员工的工资，今年经理的工资从去年的200000元增加到225000元，而其他员工的工资同去年一样，这样，这家公司所有员工今年工资的平均数和中位数与去年相比将会（ ▲ ）

    A. 平均数增加，中位数不变 B. 平均数和中位数不变

    C. 平均数不变，中位数增加 D. 平均数和中位数均增加

    A 【解析】设这家公司除经理外50名员工的工资和为a元，则这家公司所有员工去年工资的平均数是元，今年工资的平均数是元，显然＜ ；由于这51个数据按从小到大的顺序排列的次序完全没有变化，所以中位数不变．故选A．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第1、2章单元测试卷 题型：解答题

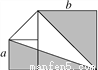
    如图所示，将面积为a2的小正方形和面积为b2的大正方形放在同一水平面上(b＞a＞0)．

    (1)用a、b表示阴影部分的面积；

    (2)计算当a＝3，b＝5时，阴影部分的面积．

    （1）；（2）. 【解析】试题分析：阴影部分是三角形，利用三角形的面积公式即可列出阴影的面积，然后再代入求值即可. 【解析】 (1)阴影部分的面积为 (2)当a=3,b =5时， .

    查看答案和解析>>

    同步练习册答案