
不透明的口袋中装有除颜色外其余均相同的2个白球、2个黄球、4个绿球,从中任取一球出来,它不是黄球的概率是( )
A.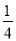 B.
B.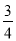 C.
C.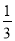 D.
D.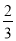
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:单选题
甲、乙、丙、丁四人进行射击测试,每人10次射击成绩平均数均是9.2环,方差分别为S甲2=0.56,S乙2=0.60,S丙2=0.50,S丁2=0.45,则成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
D 【解析】试题分析:甲、乙、丙、丁四人射击成绩的平均数均是9.2环,甲的方差是0.58,乙的方差是0.52,丙的方差0.56,丁的方差0.48,其中丁的方差最小,所以成绩最稳定的是丁.故选D.查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:填空题
某校九年级(2)班有50名同学,综合素质评价“运动与健康”方面的等级统计如图所示,则该班“运动与健康”评价等级为A的人数是_____人.
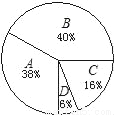
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:解答题
如图,已知△ABC三个顶点的坐标分别是A(-2,3),B(-3,-1),C(-1,1)
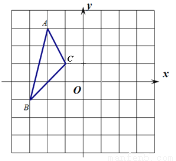
(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转180°后的△A2B2C2,并写出点A2的坐标;
(3)直接回答:∠AOB与∠A2OB2有什么关系?
【答案】(1)作图见解析,(-4,-2);(2)作图见解析,(2,-3);(3)相等.
【解析】
试题分析:(1)根据旋转的性质作图,写出点的坐标;
根据旋转的性质作图,写出点的坐标;
(3)根据旋转的性质得出结论.
试题解析:(1)作图如下,点A1的坐标(-4,-2).
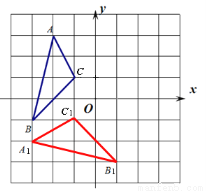
(2)作图如下,点A2的坐标(2,-3).
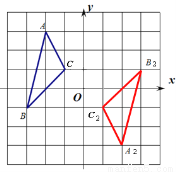
(3)相等.
考点:1.旋转作图;2.旋转的性质.
【题型】解答题
【结束】
20
已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
y=﹣5x2+2x﹣1 【解析】试题分析:根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0,由此求得m的值,进而得到该二次函数的解析式. 试题解析:依题意得:m2+m﹣4=2且m﹣2≠0. 即(m﹣2)(m+3)=0且m﹣2≠0, 解得m=﹣3, 则该二次函数的解析式为y=﹣5x2+2x﹣1查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
已知扇形的圆心角为60°,半径为2,则扇形的弧长为________(结果保留π).
【答案】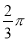
【解析】试题解析:依题意,n=60,r=2,
∴扇形的弧长= 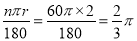 .
.
【题型】填空题
【结束】
13
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为________
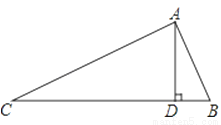
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:单选题
已知如图,圆柱OO1的底面半径为13cm,高为10cm,一平面平行于圆柱OO1的轴OO1 , 且与轴OO1的距离为5cm,截圆柱得矩形ABB1A1, 则截面ABB1A1的面积是( )
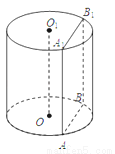
A. 240cm2 B. 240πcm2 C. 260cm2 D. 260πcm2
A 【解析】试题解析:如图所示:过点O作OC⊥AB于点C,连接BO, 由题意可得出;CO=5cm,BO=13cm, ∴BC==12(cm), ∴AB=24cm, ∴截面ABB1A1的面积是:24×10=240(cm2). 故选A.查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:解答题
如图,△ABC中,AD平分∠BAC,EG∥AD,找出图中的等腰三角形,并给出证明.
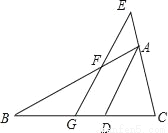
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
下列命题中,真命题是( )
A. 对角线互相垂直且相等的四边形是菱形
B. 对角线互相垂直的平行四边形是菱形
C. 对角线互相平分且相等的四边形是菱形
D. 对角线相等的四边形是菱形
B 【解析】试题分析:A.不能判断是否为菱形,故A错误; B.对角线互相垂直的平行四边形是菱形,正确; C.对角线相等且互相平分的四边形是矩形,故C错误; D.不能判断是否为菱形;故D错误; 故选B.查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市汝城县濠头学校中考数学模拟试卷 题型:单选题
如图,已知点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
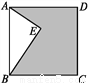
A. 48 B. 60
C. 76 D. 80
C 【解析】试题解析:∵∠AEB=90°,AE=6,BE=8, ∴AB= ∴S阴影部分=S正方形ABCD-SRt△ABE=102- =100-24 =76. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com