
已知扇形的圆心角为60°,半径为2,则扇形的弧长为________(结果保留π).
【答案】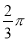
【解析】试题解析:依题意,n=60,r=2,
∴扇形的弧长= 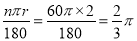 .
.
【题型】填空题
【结束】
13
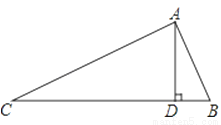
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为________
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:单选题
小朱要到距家1500米的学校上学,一天,小朱出发10分钟后,小朱的爸爸立即去追小朱,且在距离学校60米的地方追上了他.已知爸爸比小朱的速度快100米/分,求小朱的速度.若设小朱速度是x米/分,则根据题意所列方程正确的是( )
A. 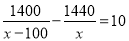 B.
B. 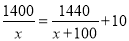
C. 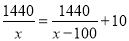 D.
D. 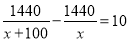
查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
如图,在平行四边形ABCD中,∠ABC和∠ADC的平分线分别交对边于点E、F,交四边形的对角线AC于点G、H.求证:AH=CG.
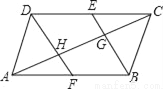
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:解答题
如图,在网格图中的△ABC与△DEF是否成位似图形?说明理由.如果是,同时指出它们的位似中心.
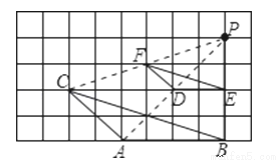
【答案】是位似图形,位似中心为P,理由见解析
【解析】试题分析:由题中的图形可以看出△ABC∽△DEF,进而又有位似中心,即可得其为位似图形.
试题解析:是位似图形,位似中心为P.
理由:∵AB∥DE,AC∥FD,
∴△ABC∽△DEF,
又其每组对应点所在的直线都经过同一个点P,
所以其为位似图形.
【题型】解答题
【结束】
25
如图①,直线y=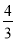 x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
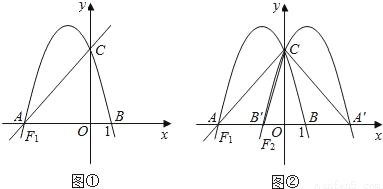
(1)求抛物线F1所表示的二次函数的表达式.
(2)若点M是抛物线F1位于第二象限图象上一点,求△AMC的面积最大时点M的坐标及S△AMC的最大值.
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)y=﹣x2﹣x+4; (2)当a=﹣时,S△AMC有最大值,最大值为9,此时,M(﹣,5); (3)当以A′、D、P为顶点的三角形与△AB′C相似时,点P的坐标为(2,0)或(﹣,0). 【解析】试题分析:(1)利用一次函数的解析式求出点A、C的坐标,然后再利用B点坐标即可求出二次函数的解析式;(2)由于M在抛物线F1上,所以可设M(a,﹣a2﹣a+4),然后分别计算S四边...查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
如图:已知点A、B是反比例函数y=﹣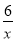 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
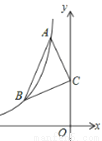
【答案】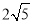
【解析】过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,如图所示.
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,由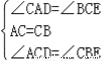 ,
,
∴△ACD≌△CBE(ASA).
设点B的坐标为(m,﹣ )(m<0),则E(0,﹣
)(m<0),则E(0,﹣ ),点D(0,3﹣m),点A(﹣
),点D(0,3﹣m),点A(﹣ ﹣3,3﹣m),
﹣3,3﹣m),
∵点A(﹣ ﹣3,3﹣m)在反比例函数y=﹣
﹣3,3﹣m)在反比例函数y=﹣ 上,
上,
 ,解得:m=﹣3,m=2(舍去).
,解得:m=﹣3,m=2(舍去).
∴点A的坐标为(﹣1,6),点B的坐标为(﹣3,2),点F的坐标为(﹣1,2),
∴BF=2,AF=4,
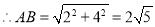
故答案为:2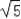 .
.
【点睛】
过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,根据角的计算得出“∠ACD=∠CBE,∠BCE=∠CAD”,由此证出△ACD≌△CBE;再设点B的坐标为(m,﹣ ),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
【题型】填空题
【结束】
18
二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
【解析】试题解析:∵二次函数有最小值﹣2, ∴y=﹣, 解得:m=.查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:单选题
不透明的口袋中装有除颜色外其余均相同的2个白球、2个黄球、4个绿球,从中任取一球出来,它不是黄球的概率是( )
A.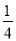 B.
B.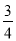 C.
C.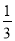 D.
D.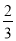
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:单选题
当A为锐角,且 <cos∠A<
<cos∠A<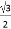 时,∠A的范围是( )
时,∠A的范围是( )
A. 0°<∠A<30° B. 30°<∠A<60° C. 60°<∠A<90° D. 30°<∠A<45°
B 【解析】试题解析:∵cos60°=, cos30°=, ∴30°<∠A<60°. 故选B.查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
若数轴上的点A、B分别与有理数a、b对应,则下列关系正确的是( )
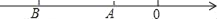
A. a<b B. ﹣a<b C. |a|<|b| D. ﹣a>﹣b
C 【解析】根据数轴的特征∵b查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市汝城县濠头学校中考数学模拟试卷 题型:填空题
如图,从点A(0,2)发出的一束光,经x轴反射,过点B(5,3),则这束光从点A到点B所经过的路径的长为_____.
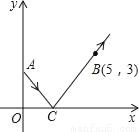
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com