
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
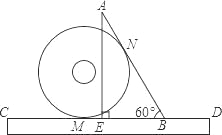
小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是 .
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:单选题
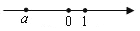
实数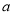 在数轴上对应的点如图所示,则
在数轴上对应的点如图所示,则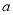 ,
, 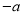 ,1的大小关系正确的是( )
,1的大小关系正确的是( )
A. 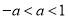 B.
B. 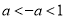 C.
C. 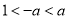 D.
D. 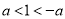
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
如上图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a﹣2b+c<0;③ac>0;④当y<0时,x<﹣1或x>2.其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4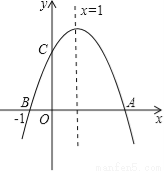
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
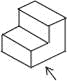
如图是由我市某中学楼层间的两个台阶组成的几何体,已知两个台阶的高度和宽度是相同的,据此可判断此几何体的三视图是( ).
A. 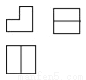
B. 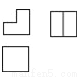
C. 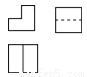
D. 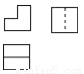
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
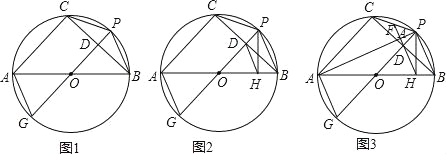
⊙O是△ABC的外接圆,AB是直径,过 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP;
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG;
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2 ,求AC的长.
,求AC的长.
【答案】(1)证明见解析;
(2)证明见解析;
(3)AC=10
【解析】
试题分析:(1)利用等弧所对的圆周角相等即可求解;
(2)利用等弧所对的圆周角相等,得到角相等∠APG=∠CAP,判断出△BOD≌△POH,再得到角相等,从而判断出线平行;
(3)由三角形相似,得出比例式,△HON∽△CAM, ,再判断出四边形CDHM是平行四边形,最后经过计算即可求解.
,再判断出四边形CDHM是平行四边形,最后经过计算即可求解.
试题解析:(1)∵过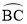 的中点P作⊙O的直径PG,
的中点P作⊙O的直径PG,
∴CP=PB,
∵AB,PG是相交的直径,
∴AG=PB,
∴AG=CP;
(2)证明:如图 2,连接BG
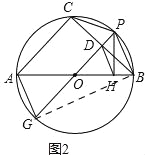
∵AB、PG都是⊙O的直径,
∴四边形AGBP是矩形,
∴AG∥PB,AG=PB,
∵P是弧BC的中点,
∴PC=BC=AG,
∴弧AG=弧CP,
∴∠APG=∠CAP,
∴AC∥PG,
∴PG⊥BC,
∵PH⊥AB,
∴∠BOD=90°=∠POH,
在△BOD和△POH中,
 ,
,
∴△BOD≌△POH,
∴OD=OH,
∴∠ODH= (180°﹣∠BOP)=∠OPB,
(180°﹣∠BOP)=∠OPB,
∴DH∥PB∥AG.
(3)如图3,作CM⊥AP于M,ON⊥DH于N,
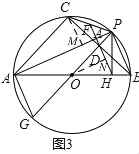
∴∠HON= ∠BOP=
∠BOP= ∠COP=∠CAP,
∠COP=∠CAP,
∴△HON∽△CAM,
∴ ,
,
作PQ⊥AC于Q,
∴四边形CDPQ是矩形,
△APH与△APQ关于AP对称,
∴HQ⊥AP,
由(1)有:HK⊥AP,
∴点K在HQ上,
∴CK=PK,
∴PK是△CMP的中位线,
∴CM=2FK=4,MF=PF,
∵CM⊥AP,HK⊥AP,
∴CM∥HK,
∴∠BCM+∠CDH=180°,
∵∠BCM=∠CAP=∠BAP=∠PHK=∠MHK,
∴∠MHK+∠CDH=180°,
∴四边形CDHM是平行四边形,
∴DH=CM=4,DN=HN=2,
∵S△ODH= DH×ON=
DH×ON= ×4×ON=2
×4×ON=2 ,
,
∴ON= ,
,
∴OH=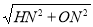 =5,
=5,
∴AC= =10.
=10.
考点:圆的综合题.
【题型】解答题
【结束】
16
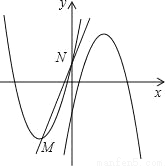
如图,在平面直角坐标系中,已知抛物线C1:y= 的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.
的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.
(1)结合图象,直接写出不等式 x2+6x+2<kx+b的解集;
x2+6x+2<kx+b的解集;
(2)若抛物线C2的顶点与点M关于原点对称,求p的值及抛物线C2的解析式;
(3)若直线l沿y轴向下平移q个单位长度后,与(2)中的抛物线C2存在公共点,
求3﹣4q的最大值.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
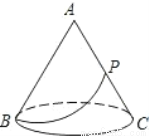
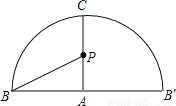
如图有一圆锥形粮堆,其主视图是边长为6m的正三形ABC。
(1)求该圆锥形粮堆的侧面积。
(2)母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,求小猫经过的最短路程。 (结果不取近似数)
【答案】(1) 18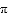
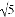 m.
m.
【解析】试题分析:(1)根据圆锥的侧面展开图是扇形,圆锥的侧面积公式是π×底面圆半径×圆锥的母线长;扇形的面积公式是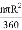 ,进行计算即可;
,进行计算即可;
(2)根据两点之间,线段最短.首先要展开圆锥的半个侧面,再连接BP.发现BP是直角边是3和6的直角三角形的斜边.根据勾股定理即可计算.
试题解析:(1)根据圆锥的侧面积等于展开扇形的面积得:
πrl=π×3×6=18π.
(2)圆锥的底面周长是6π,则6π=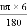 ,
,
∴n=180°,即圆锥侧面展开图的圆心角是180度.
则在圆锥侧面展开图中AP=3,AB=6,∠BAP=90度.
∴在圆锥侧面展开图中BP=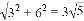 m.
m.
故小猫经过的最短距离是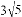 m.
m.
【题型】解答题
【结束】
9
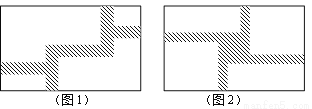
(1)如图1,在一块宽为12m,长为20m的矩形地面上修筑同样宽的道路,余下的部分种上草坪.要使草坪的面积为180m2,求道路的宽;
(2)现在对该矩形区域进行改造,如图2,在正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行的且宽度相等的道路,已知道路的宽为正方形边长的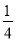 .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的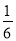 ,求道路的宽.
,求道路的宽.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 七年级数学 小题易丢分 题型:填空题
小明做作业时,不小心将方程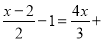 ●中的一个常数污染了看不清楚,小芳告诉他该方程的解是负数,并且这个常数是负整数,该方程的解是_______.
●中的一个常数污染了看不清楚,小芳告诉他该方程的解是负数,并且这个常数是负整数,该方程的解是_______.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(A卷) 题型:单选题
已知一粒米的质量是0.000021千克,这个数用科学记数法表示为( )
A. 21×10-4 B. 2.1×10-6 C. 2.1×10-5 D. 2.1×10-4
C 【解析】由题意得0.000021=2.1×10-5,所以选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com