
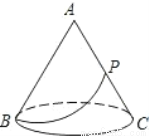
如图有一圆锥形粮堆,其主视图是边长为6m的正三形ABC。
(1)求该圆锥形粮堆的侧面积。
(2)母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,求小猫经过的最短路程。 (结果不取近似数)
【答案】(1) 18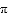
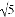 m.
m.
【解析】试题分析:(1)根据圆锥的侧面展开图是扇形,圆锥的侧面积公式是π×底面圆半径×圆锥的母线长;扇形的面积公式是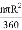 ,进行计算即可;
,进行计算即可;
(2)根据两点之间,线段最短.首先要展开圆锥的半个侧面,再连接BP.发现BP是直角边是3和6的直角三角形的斜边.根据勾股定理即可计算.
试题解析:(1)根据圆锥的侧面积等于展开扇形的面积得:
πrl=π×3×6=18π.
(2)圆锥的底面周长是6π,则6π=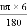 ,
,
∴n=180°,即圆锥侧面展开图的圆心角是180度.
则在圆锥侧面展开图中AP=3,AB=6,∠BAP=90度.
∴在圆锥侧面展开图中BP=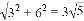 m.
m.
故小猫经过的最短距离是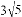 m.
m.
【题型】解答题
【结束】
9
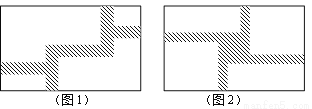
(1)如图1,在一块宽为12m,长为20m的矩形地面上修筑同样宽的道路,余下的部分种上草坪.要使草坪的面积为180m2,求道路的宽;
(2)现在对该矩形区域进行改造,如图2,在正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行的且宽度相等的道路,已知道路的宽为正方形边长的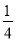 .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的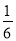 ,求道路的宽.
,求道路的宽.
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C. 抛一个质地均匀的正六面体骰子,向上的面点数是5
D. 抛一枚硬币,出现反面的概率
B 【解析】试题解析:A、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为,不符合题意; B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率是,符合题意; C、抛一个质地均匀的正六面体骰子,向上的面点数是5的概率为,不符合题意; D、抛一枚硬币,出现反面的概率为,不符合题意, 故选B.查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:填空题
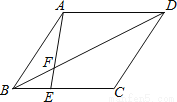
(2010•沈阳)如图,在?ABCD中,点E在边BC上,BE:EC=1:2,连接AE交BD于点F,则△BFE的面积与△DFA的面积之比为 .
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
﹣5的倒数的相反数是( )
A. 5 B. 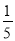 C. ﹣5 D. ﹣
C. ﹣5 D. ﹣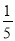
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
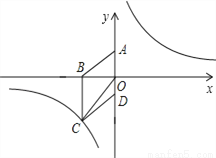
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且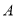 (0,3)、
(0,3)、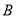 (﹣4,0).
(﹣4,0).
(1)求经过点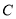 的反比例函数的解析式;
的反比例函数的解析式;
(2)设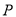 是(1)中所求函数图象上一点,以
是(1)中所求函数图象上一点,以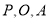 顶点的三角形的面积与△COD的面积相等.求点P的坐标.
顶点的三角形的面积与△COD的面积相等.求点P的坐标.
【答案】(1)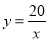 ;(2)P(
;(2)P(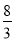 ,
, 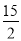 )或(-
)或(-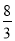 ,-
,-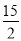 ).
).
【解析】试题分析:综合考查反比例函数及菱形的性质,注意:根据菱形的性质得到点C的坐标;点P的横坐标的有两种情况.
(1)根据菱形的性质可得菱形的边长,进而可得点C的坐标,代入反比例函数解析式可得所求的解析式; (2)设出点P的坐标,易得△COD的面积,利用点P的横坐标表示出△PAO的面积,那么可得点P的横坐标,就求得了点P的坐标.
试题解析:(1)由题意知,OA=3,OB=4,
在Rt△AOB中,AB=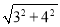 =5,
=5,
∵四边形ABCD为菱形,
∴AD=BC=AB=5,
∴C(-4,-5).
设经过点C的反比例函数的解析式为y=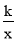 (k≠0),
(k≠0),
则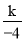 =-5,解得k=20.
=-5,解得k=20.
故所求的反比例函数的解析式为y=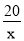 .
.
(2)设P(x,y),
∵AD=AB=5,OA=3,
∴OD=2,S△COD=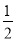 ×2×4=4,
×2×4=4,
即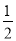 •OA•|x|=4,
•OA•|x|=4,
∴|x|=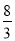 ,
,
∴x=±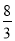 ,、
,、
当x=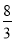 时,y=
时,y=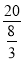 =
=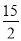 ,当x=-
,当x=-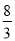 时,y=
时,y=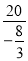 =-
=-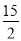 ,
,
∴P(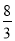 ,
, 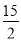 )或(?
)或(?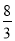 ,?
,?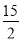 ).
).
考点:反比例函数综合题.
【题型】解答题
【结束】
14
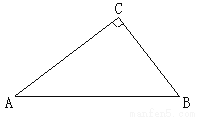
如图,在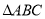 中,
中, 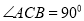 ,点
,点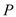 到
到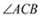 两边的距离相等,且
两边的距离相等,且 .
.
(1)先用尺规作出符合要求的点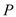 (保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(2)设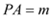 ,
,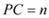 ,试用
,试用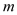 、
、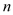 的代数式表示
的代数式表示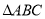 的周长和面积;
的周长和面积;
(3)设 与
与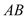 交于点
交于点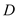 ,试探索当边
,试探索当边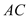 、
、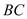 的长度变化时,
的长度变化时,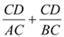 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
设a是方程x2﹣2006x+1=0的一个根,求代数式a2﹣2007a+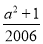 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 七年级数学 小题易丢分 题型:填空题
我们知道,无限循环小数都可以转化为分数.例如:将0. 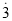 转化为分数时,可设0.
转化为分数时,可设0. 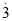 =
= 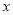 ,则
,则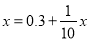 ,解得
,解得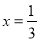 ,即0.
,即0. 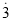 =
=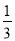 .仿此方法,将0.
.仿此方法,将0. 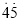 化成分数是_______.
化成分数是_______.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 七年级数学 小题易丢分 题型:单选题
如图,下列一束束“鲜花”都是由一定数量形状相同且边长为1的菱形按照一定规律组成,其中第①个图形含边长为1的菱形3个,第②个图形含边长为1的菱形6个,第③个图形含边长为1的菱形10个,... ...,按此规律,则第⑦个图形中含边长为1的菱形的个数为( )
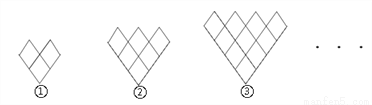
A. 36 B. 38 C. 34 D. 28
A 【解析】试题解析:∵第①个图形含边长为1的菱形1+2=3个, 第②个图形含边长为1的菱形1+2+3=6个, 第③个图形含边长为1的菱形1+2+3+4=10个, …, ∴第n个图形中含边长为1的菱形的个数为1+2+3+4+…+n+(n+1)=(n+1)(n+2), ∴第⑦个图形中含边长为1的菱形的个数为1+2+3+4+5+6+7+8=36. 故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级北师大版数学试卷(B卷) 题型:解答题
某城市对居民用水实行阶梯收费,每户每月用水量如果未超过20吨.按每吨1.9元收费;每户每月用水量如果超过20吨,未超过的部分仍按每吨1.9元收费,超过的部分则按每吨2.8元收费.设某户每月的用水量为x吨,应收水费为y元
(1)分别写出每月用水量未超过20吨和超过20吨,y与x间的函数关系式.
(2)若该城市某户居民5月份水费平均为每吨2.2元,问该户居民5月份用水多少吨?
(1)y=2.8x﹣18;(2) 该户居民5月份用水30吨. 【解析】试题分析:(1)分别根据:未超过20吨时,水费y=1.9×相应吨数;超过20吨时,水费y=1.9×20+超过20吨的吨数×2.8;列出函数解析式; (2)由题意知该户的水费超过了20吨,根据:1.9×20+超过20吨的吨数×2.8=用水吨数×2.2,列方程求解可得. 试题解析::(1)当0≤x≤20时,y=1.9x...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com